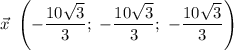Длина вектора в равна 10. Вычислите координаты
этого вектора, если известно, что все они равны.
Другие вопросы по теме Математика
Популярные вопросы
- надо очень сижу на уроке и учитель спрашивает меня...
2 - 8. Дайте характеристику діяльності Юлія Цезаря...
3 - Відновіть і запишіть фразеологізми, уставивши потрібні слова. Направо й...
3 - Запишіть рівняння реакцій перетворень: Na → Na2O → NaOH → Na2SO4 →NaCl P...
2 - Анализ экологической ситуации на Луганщине и прогнозирование ее возможных...
2 - Нужен небольшой текст-рассуждение(примерно 80-100 слов) отвечающий на вопрос:...
3 - Реферат на тему: Історія відкриття збереження енергії .. ів ,потрібно на...
3 - На фото все показано.Буду дуже вдячна за вашу до...
1 - Рикии тикки Тави краткое содержание ,но побольше...
2 - Today you ll write an article to a school newspaper about air travel...
2
Имеем вектор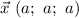 , длина которого
, длина которого 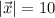
Значит,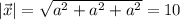
ответ: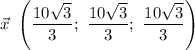 или
или