Длина гипотенузы прямоугольного треугольника 16,4 cм один из прилегающих к ней острых углов равен 60(градусов).найдите длину длину одного из его катетов и определите наибольшее число , которому может соответствовать другой катет

14,2

Пошаговое объяснение:

пусть угол А = 60, тогда угол В равен 30. Катет, который лежит напротив угла 30 градусов равен половины гипотенузы. АС=1/2АВ= 8,2см

За т. Пифагора  ВС =14,2 см

8,2 и √201,72

Пошаговое объяснение:

Пусть есть прямоугольный треугольник ABC с прямым углом A и гипотенузой BC=16,4 см.

1) Первый случай: ∠x=60°. Тогда по теореме о сумме углов треугольника ∠y=180°-90°-∠x=90°-60°=30°. По свойству катета, противолежащего углу в 30°, AB=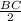==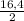8,2

По теореме Пифагора BC²=AB²+AC². Выразим отсюда AС:

AC=√(BC²-AB²) = √(16,4²-8,2²) = √(268,96-67,24) = √201,72

2) Если рассмотрим случай, когда ∠y=60°, то просто катеты поменяются значениями