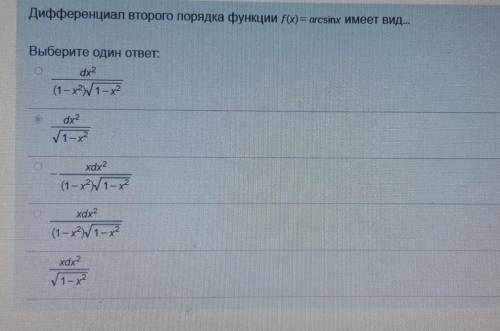
Дифферинциал второго порядка функции f(x)=arcsinx имеет вид??
Другие вопросы по теме Математика
Популярные вопросы
- Є два види сталі :одна з великою залишковою індукцією, друга - з порівняно незначною....
3 - Человек нажимает на лопату силой 500 н. Какое давление оказывает лопата на почву,...
3 - Превратите текст в время(Präteritum) Früh morgens hat Lea ihr Wohnzimmer aufgeräumt....
2 - По во истории высказываются различные, часто противоречивыеточки зрения. Ниже приведена...
1 - Два маляра красили забор. Первый покрасил 2/3 забора, второй – на 2/5 забора меньше....
1 - Сделать буктрейлер до твору О.Генрі Дари волхвів...
2 - В чем счастье и трагедия Ромео и Джульета?...
1 - На лампочке накаливания написано «36 В; 15 Вт». Вычисли электрическое сопротивление...
1 - Найдите все значения переменной, при которых двучлен 3x-x^2 принимает не отрицательные...
3 - Опишите растение элодею (см. рисунок) по следующему плану: группа растений; жизненная...
3
Дифференциал второго порядка – это вторая производная функции. Первая производная показывает, как меняется функция, а вторая производная – как меняется скорость изменения функции.
Функция arcsinx – это обратная функция синусу. Она обозначается так: f(x) = arcsinx.
Теперь давайте найдем первую производную функции f(x).
f(x) = arcsinx
f'(x) = d/dx (arcsinx)
Чтобы найти первую производную функции arcsinx, мы должны использовать цепное правило. Цепное правило состоит в том, чтобы взять производную внутренней функции и умножить ее на производную внешней функции.
Так как внутренняя функция – это sinx, а внешняя – это arcsinx, то:
f'(x) = (cosx) * (1 / √(1 - sin^2x))
Теперь давайте найдем вторую производную функции f(x).
f''(x) = d/dx ((cosx) * (1 / √(1 - sin^2x)))
Мы снова используем цепное правило. Найдем производную внутренней функции (cosx) и умножим ее на производную внешней функции (1 / √(1 - sin^2x)), после чего сложим с произведением производной внутренней функции и внешней функции (sinx) умноженными на производную векторной функции (1 / √(1 - sin^2x))^2.
f''(x) = (-sinx) * (1 / √(1 - sin^2x)) + (cosx) * ((-sinx)(2 / (1 - sin^2x)))
Упростим это выражение:
f''(x) = (-sinx) / √(1 - sin^2x) + (-sinx)(2cos^2x) / (1 - sin^2x)
Теперь у нас есть ответ на вопрос: дифференциал второго порядка функции f(x) = arcsinx имеет вид:
f''(x) = (-sinx) / √(1 - sin^2x) + (-sinx)(2cos^2x) / (1 - sin^2x)
Надеюсь, это решение понятно и полно для школьника. Если возникнут вопросы, пожалуйста, сообщите.