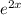Дифференцированные уравнения.
Найти общее решение уравнения.
y'+2*y=(x^2)-x
Полное решение, чем подробнее тем лучше. За ранее если очень выручите.
Другие вопросы по теме Математика
Популярные вопросы
- Як зміниться ємність повітряного конденсатора, якщо відстань між пластинами...
1 - Задание 2: Рассмотрите ситуации в таблице. Впишите в таблицу источник, приемник...
1 - Сложные вещества образованы не одним, а двумя и более химическими элементами....
1 - На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G и H. По каждой...
2 - Молярна маса електроліту, який містить йони Ме+ сульфат-іони, становить 342...
2 - Что добавляли в Парик женщины Древнего Египта...
3 - на рисунке изображены силы F1 и F2 пол действием которых движется тело с ускорением...
2 - Мақсат зерттеуінде нені пайдаланды және қандай тұжырым жасады? Табиғала бақылау...
1 - Перерисуйте в зошит трикутники, зображені на рисунку 121, проведітьу кожному...
2 - Английский английский ХАЛЯЩИВКОВ В БАН)...
2
Умножим обе части уравнения на