Дифференциальные уравнения решить , очень нужно!
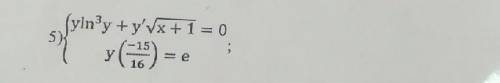
Другие вопросы по теме Математика
Популярные вопросы
- Придумайте сказку на тему мы великие...
1 - Втреугольнике авс сторона ав в 2 раза больше стороны вс и на 5 см меньше...
3 - Лишайники являются индикаторами чистоты воздуха. представители какого морфологического...
2 - Что за человек гродничий? какой он городоначальник? каков его город? (ревизор...
2 - 1)два пешехода вышли одновременно навстречу друг другу из 2 сей, расстояние...
3 - Сколько в числе 605840 единиц 1 класса...
1 - 1) объясни вычисления в каждом случае и закончи их 8.484: 4=8.000: 4+400:...
3 - 2-3 от 3-9 этого числа равно 14 это дробь найди это число и напишите как...
3 - Врешением! на старой липе в чёрных её ветвях остались только редкие золотые...
1 - Подобрать однокоренные слова к слову снег...
1
общее решение
частное решение