Дифференциальные уравнения 2 порядка
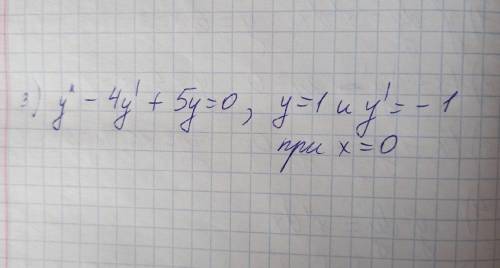
Другие вопросы по теме Математика
Популярные вопросы
- В посёлке за 3 года было построено 73 жилых дома. В первый год было построено...
2 - Англійська мова. До ть вправа на фото....
2 - ответьте полностью на 3 задание...
2 - Напишите рассказ о моём имени Алина и фамилии Ошева...
3 - Отримати саліцилової кислоти з кальцій карбіду...
1 - В магазин привезли фрукты к вечеру продали 32% всех фруктов составляют 480...
1 - Стратегические приоритеты национальных интересов и национальной безопасности...
1 - Цінності час, особа ,число, рід(якщо є)...
3 - Янис бежит со скоростью 2 м/с. Вычисли, сколько километров он пробежит за...
1 - У якому випадку на повне окиснення зазначеної порції речовини витратиться...
1
Замена:
общее решение.
В систему:
Частное решение