Дифференциальное уравнение! Сделать до пн.!
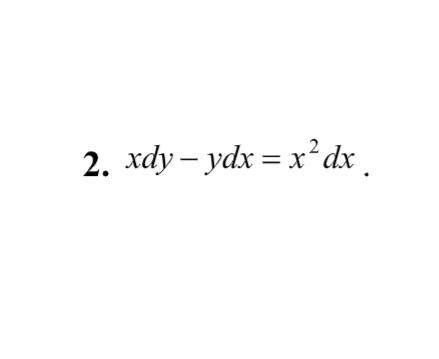
Другие вопросы по теме Математика
Популярные вопросы
- Возможно ли разделить нечетное число на четное? !...
3 - Чому нас навчають євангельські притчі?...
1 - Представьте, что клетка- это большой город. с какими структурами города можно сравнить...
3 - Зелёный цвет растению придаёт пигмент клетке растения он находится в--...
3 - Составить диалог о ласточкином гнезде...
2 - Найти закономерность и заполнить пустые клетки 1 строка: ? 300000 2 строка: 289573...
3 - Стальной стержень массой 600г нагреть от 20с до 1020с на сколько увеличилось внутренняя...
2 - Отрезок мn имеет длину х см (рис.15). начертите отрезок ав. длина которого равна...
1 - 1. царь петр | прорубил это в европу это бывает на экране при работе компьютера...
2 - На классной доске записаны 12 слов. треть этих слов петя списал в тетрадь неверно...
3
Пошаговое объяснение:
xdy - ydx = x² dx
будем решать как линейное дифференциальное уравнение
xdy - ydx - x² dx =0
делим все на xdx
это неоднородное уравнение
сделаем замену переменных
y=ux; y' = u'x + u.
получим
приведем к общему знаменателю и приравняем полученный числитель к 0
или
u'x-x=0 ⇒ u' = 1 интегрируем
∫u'du = ∫1dx
u = x + C
а у нас было у = ux, тогда получается
y = ux = x² + Cx