Дифференциальное уравнение
решить
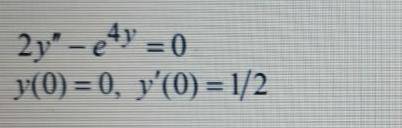
Другие вопросы по теме Математика
Популярные вопросы
- Как Васютка догадался, что рядом река? Вдалеке у реки рос лиственный...
3 - Решите каждое неравенство: х 9;х 12;х 5;х 3...
1 - геометрия 8 класс с решение...
1 - Выполните сложение и вычитание алгебраических дробей:...
1 - Если t= 19,8, то значение выражения |t|= Положителное или отрицательное...
2 - 3. В каком ряду во всех словах пропущена одна и та же буква? А) сия..шь,...
2 - нужно составить предложения, используя фразы Make sentences that are...
1 - 1. В чем заключается решение дифференциальных уравнений методом Эйлера?...
3 - 1. Розв’яжіть рівняння: а) 36х – х² = 0; б) 3х² – 12 = 0; в) 2х² –...
2 - Сочинение на тему ли наших животных Красная книга...
1
Частное решение найти , имея такое общее решение, сложнее, чем найти это общее решение. Там надо сложную систему уравнений решать . Поэтому, я думаю, что описка в условии. Смотри ниже .