1. Математика
  2. Дифференциальное уравнение найти

Дифференциальное уравнение найти частное решение удовлетворяющее заданному начальному уравнению dy/dx=5e^2x/y^2

qqqqq9 qqqqq9    1   31.07.2019 09:40    0

Ответы
SofyaA3 SofyaA3  31.08.2020 06:56
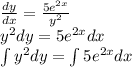
\frac{dy}{dx}=\frac{5e^{2x}}{y^2}\\ y^2dy = 5e^{2x}dx\\
\int y^2dy = \int 5e^{2x}dx
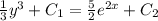
\frac{1}{3}y^3+C_1= \frac{5}{2}e^{2x}+C_2
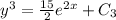
y^3= \frac{15}{2}e^{2x}+C_3
y= \sqrt [3] {\frac{15}{2}e^{2x}} - частное решение
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
базарганово базарганово  25.09.2019 14:50
Укамиля иназрин вместе 20манатукамиляв3р ск. денег у каждого...
Topxic Topxic  25.09.2019 14:50
3друга алеша коля и саша сели на скамейку в один ряд . сколькими они смогли это сделать?...
fbgudcc fbgudcc  25.09.2019 14:50
Решите систему уравнений y+2x=6 3x^2-y^2=3...
didar6 didar6  25.09.2019 14:50
Вычислите : 14 целых 12/17 - (6 целых 8/17 + 3 целых 3/17)...
2007628475626 2007628475626  25.09.2019 14:50
Аня задумала число ,умножила его на 6 и к произведению прибавила 34 . в результате получила 127. какое число задумала аня...
ПЕДРО12 ПЕДРО12  25.09.2019 14:50
Составьте систему уравнений решите её подстановки: три тетради и две ручки стоит 230 тг. 8 тетрадей дороже одной ручки на 170тг. сколько стоит одна тетрадь? сколько стоит...
ghigalskiidani ghigalskiidani  25.09.2019 14:50
Во сколько раз 100 больше 0,01? скажите )...
Гогич Гогич  25.09.2019 14:50
Решите уравнение 18,63÷(4,3+1,2х)=2,3...
мыпоммрт мыпоммрт  25.09.2019 14:50
8т 30 кг 8 у 3кг 42 км 4020 м 5 м 20 сек 520 сек сравните...
zeralskaya zeralskaya  25.09.2019 14:50
Построй треугольник мкр м(-3; 5) к(3; 0)р(0; -5)...

Популярные вопросы