1. Математика
  2. Дифференциация. Какой вариант

Дифференциация. Какой вариант решения правильный 1 или 2 или оба?


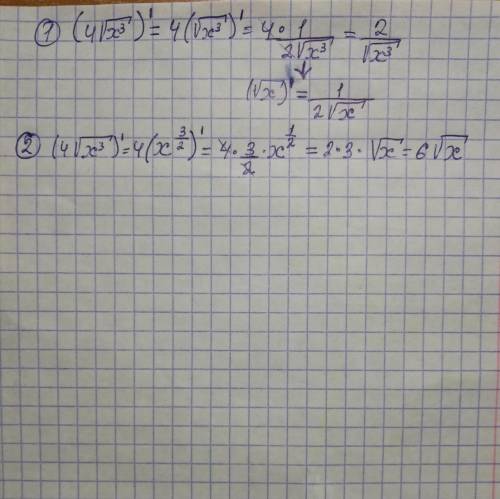
Дифференциация. Какой вариант решения правильный 1 или 2 или оба?

Be11a Be11a    3   10.09.2020 22:29    1

Ответы
nastiakosovic nastiakosovic  15.10.2020 20:07

В первом случае ошибка в том, что при дифференцировании сложной функции  вы не умножили производную внешней функции - корня, на производную внутренней функции -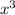 x^3 .

Надо пользоваться формулой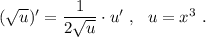  (\sqrt{u})'=\dfrac{1}{2\sqrt{u}}\cdot u'\ ,\ \ u=x^3\ .

(4\sqrt{x^3})'=4\cdot (\sqrt{x^3})'=4\cdot \dfrac{1}{2\sqrt{x^3}}\cdot (x^3)'=2\cdot \dfrac{1}{\sqrt{x^3}}\cdot 3x^2=\\\\=6\cdot \dfrac{x^2}{\sqrt{x^3}}=6\cdot x^{2-\frac{3}{2}}=6\cdot x^{\frac{1}{2}}=6\sqrt{x}

Во втором случае функцию записываем таким образом, чтобы избежать сложной функции . Получили простую степенную функцию с показателем 3/2 .

(4\sqrt{x^3})'=4\cdot (x^{\frac{3}{2}})'=4\cdot \dfrac{3}{2}\cdot x^{\frac{3}{2}-1}=6\cdot x^{\frac{1}{2}}=6\sqrt{x}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
2000nmz 2000nmz  02.06.2019 13:00
Встретил волк красную шапочку и спрашивает: сколько пирожков несешь в корзине, красная шапочка? . я положила в корзину сначала две третьих количества пирожков, а затем еще...
miku1368 miku1368  02.06.2019 13:00
:для посадки закупили 240 саженцев клена, 1/4 часть саженцев садили. сколько саженцев посадили? напишите решение...
favorit19971 favorit19971  02.06.2019 13:00
Самолет вылетел с аэропорта со скоростью 500км в час через два часа с этого же аэропорта в том же направление вылетел другой самолет со скоростью 700 км в час сколько километров...
stanislavcoola stanislavcoola  02.06.2019 13:00
Вычислите: 3/8*3*1/9-2*1/2/3*3/4+5*1/3...
pashalol3 pashalol3  02.06.2019 13:00
Уваси было 50 рублей. когда он купил 2 одинакого стоющие ручки у него осталось 22 рубля. сколько рублей стоит 1 ручка?...
Валерия3365 Валерия3365  02.06.2019 13:00
30: 5*6+29=30 правильно поставить скобки...
BatsonPlay BatsonPlay  02.06.2019 13:00
Проверьте справедливость равенства а) 1/2=5/10; б)1/5=2/10...
Education26 Education26  02.06.2019 13:00
А6. выбери то выражение, с которого можно узнать, сколько лапок у 5 черепах? 1. 4+5; 2. 4 · 5; 3. 4 · 5 + 5....
danilkalmykov1 danilkalmykov1  02.06.2019 13:00
Решить : 6-5х=-9х-2 2(5х-1)+8=6 4+5(3х-4)=7х-8 6(3х+4)-5(4х-3)=29 2х-4(7х-3)=10-5(3х-7) 11(2х-3)=5(4х-6)+2х...
КаМиЛлА2911 КаМиЛлА2911  02.06.2019 13:00
Постройте угол авс=40 градусов. отложите на стороне ва отрезок вд=2 см. найдите расстояние от точки д до стороны вс?...

Популярные вопросы