1. Математика
  2. Диф. уравнения. Дано уравнение

Диф. уравнения. Дано уравнение y"+p*y'+q*y=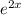e^{2x} , у его характерного уравнения есть корни k1 = 1, k2 = -2. Указать вид отдельного решения y⁻⁻ (соре за то, что условие такое непонятное, переводила с украинского)

rockmus rockmus    3   04.07.2021 01:46    3

Ответы
aium08 aium08  03.08.2021 02:06

Задано линейное неоднородное дифференциальное уравнение 2 порядка с постоянными коэффициентами (ЛНДУ 2 пор.). И заданы корни характеристического многочлена . Указать вид частного решения ЛНДУ 2 порядка по виду правой части этого уравнения .

y''+py'+qy=e^{2x}\ \ ,\ \ \ k_1=1\ ,\ k_2=-2\\\\f(x)=e^{2x}=e^{2\cdot x}\cdot 1\ \ \Rightarrow \ \ \ \alpha =2\ne k_1\ne k_2\ \ \Rightarrow \ \ \ x^{s}=x^0\\\\y_{chastnoe\ neodnorodn.}=e^{2\cdot x}\cdot A\cdot x^0\\\\y_{chastnoe\ neodnorodn.}=A\cdot e^{2x}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
MiliitVel1 MiliitVel1  15.12.2021 11:25
А)2 3/7 *7 б) (2/9 +1 2/3)*3 в...
Glenchittt1 Glenchittt1  15.12.2021 11:25
Найди периметр прямоугольника сторона якого доривнюе 6 см и 5 см...
usachiovavika usachiovavika  15.12.2021 11:25
решить раскрой скобки и упрости выражение:-(7-а)-23...
rinnavinn rinnavinn  15.12.2021 11:25
с контрольной работой по математике на тему «элементы комбинаторики» >...
vyachik2000 vyachik2000  15.12.2021 11:25
Татьяна должна обсудить свою новую идею с директором, бухгалтером и программистом. С каждым из них обсуждение длится ровно час. Известно, что директор занят с 10 до 12 часов,...
катяkfrr катяkfrr  15.12.2021 11:25
A) 12x + 4 + 6x +30 6) 12- (2x +12) упрастите...
Илья2519 Илья2519  15.12.2021 11:28
3 5/8: 5 какой ответ мне И 2 2/3:1 1/7...
lenababkina200 lenababkina200  15.12.2021 11:28
6 Рассмотри и объясни разные нахождения площади фигуры, вырезанной из прямоугольника. Щас фотку скину быстрей...
alkofner alkofner  15.12.2021 11:28
-х-(2у+4) Раскройте скобки 0,13+(-5с+а) Приводите подобные слагаемые 3,7х+2,8у+5х+4,9у 0,7с-7а+4с-3...
VERLIA VERLIA  15.12.2021 11:28
Решение задач на умножение смешанных дробей Найди значение выражения...

Популярные вопросы