Диф. уравнения. Дано уравнение y"+p*y'+q*y=2x+3 , у его характерного уравнения есть корни k1 = 0, k2 = 4. Указать вид отдельного решения y⁻⁻ (соре за то, что условие такое непонятное, переводила с украинского)
Другие вопросы по теме Математика
Популярные вопросы
- Abcd - трапеция. ac перпендикулярно bd. bc=4 см ad=16 см ao=8 см...
2 - Газовый пистолет не совершено летнему можно купить? и где? ...
1 - Чему равна гипотенуза противолежащая углу 90 и 60 градусов? ...
1 - Найдите массу сульфата меди 2 в 50 г медного купороса...
2 - Моя учительница по технологии отменила суммарно за 2-ую четверть...
3 - Дано комплексное число a. требуется: 1) записать число a в и тригонометрической...
2 - Рассчитайте массовую и мольную концентрацию раствора, полученного...
3 - Какую массу железного купороса надо добавить к 300 г 7% раствора...
3 - Можете ответить на вопросы только эти вопросы нужно выписать из...
1 - Юридическая психология,вдруг кто-то осужденный м. посещал сеансы...
3
Если нужно лишь указать вид "отдельного" (полагаю что подразумевается частное) решения, то существует специальное правило (прикрепленный файл)
В данном случае неоднородность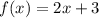
у которой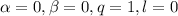
Таким образом частное решение имеет вид:
Если нужно лишь указать вид "отдельного" (полагаю что подразумевается частное) решения, то существует специальное правило (прикрепленный файл)
В данном случае неоднородность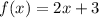
у которой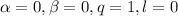
Таким образом частное решение имеет вид: