Диагональ грани куба равна 2корень из 6. найдите диагональ куба
Другие вопросы по теме Математика
Популярные вопросы
- 1. в каком ряду все слова являются однокоренными? 1) печать, печатей...
1 - Укажите уравнение, которое не имеет корней. 1) 9.1x^2+4.5=0; 2) 9.1x^2+4.5x=0;...
3 - Вставить буквы в слова у*кой , доро*кой , ре*кий , холо* ,...
1 - Уважаемые ! , мне с вопросами, возникшими у меня по . ответы жду правильные...
1 - Определить кпд электрического двигателя мощностью 7,36 квт,если он работает...
3 - Надо как решить примеры: 37+(-20)+(-24)+(-46)= -17+(-2,9)+(+2,74)+(-6,13)=...
1 - Обведи номер предложения, в котором есть глагол в форме настоящего времени,=(=(...
2 - Сна и как произносится eagle dolphin whale snake camel...
1 - Докажите, что условия тильзитского мирного договора были крайне невыгодны...
3 - Основной оксид sro+h2so4 = основной оксид + кислотный оксид sro+so3=...
3
ответ: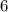
Пусть ребро куба - это . Тогда, по теореме Пифагора (сумма квадратов катетов равна квадрату гипотенузы), верно следующее (катеты прямоугольного треугольника приняты за ребра куба, а гипотенуза - за диагональ грани куба):
. Тогда, по теореме Пифагора (сумма квадратов катетов равна квадрату гипотенузы), верно следующее (катеты прямоугольного треугольника приняты за ребра куба, а гипотенуза - за диагональ грани куба):
И тогда диагональ куба принимает следующее значение (опять же теорема Пифагора: катеты - ребро и диагональ грани, а гипотенуза - главная диагональ нашего куба):
Значит, диагональ куба (гипотенуза) равна