1. Математика
  2. Детектор лжи фиксирует неверный

Детектор лжи фиксирует неверный ответ с вероятностью 95%. Какова вероятность того, что на 10 поставленных вопросов неправильный ответ будет зафиксирована хотя бы два раза?

Mirajanesan Mirajanesan    3   29.10.2020 16:36    0

Ответы
tayatoadvel tayatoadvel  28.11.2020 16:38

0.99999999998134765625

Пошаговое объяснение:

Тут нужно воспользоваться формулой Бернулли, описывающей вероятность того, что в n независимых испытаниях, в каждом из которых вероятность наступления события равна p, событие наступит ровно k раз.

P_n(k)=C_n^k \cdot p^k\cdot (1-p)^{n-k}

Будем решать задачу от обратного. Найдем вероятность противоположного события, а именно: вероятность того, что неправильный ответ будет зафиксирован 0 или 1 раз.

Для такой задачи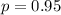 p=0.95

P_{10}(0)=C_{10}^0 \cdot p^0\cdot (1-p)^{10-0}=\frac{10!}{0!\cdot(10-0)!}\cdot 0.95^0\cdot (1-0.95) ^{10}=1\cdot1\cdot0.05^{10}

P_{10}(1)=C_{10}^1 \cdot p^1\cdot (1-p)^{10-1}=\frac{10!}{1!\cdot(10-1)!} \cdot 0.95^1\cdot 0.05^9=10\cdot 0.95\cdot 0.05^9

Тогда вероятность того, что ответ будет зафиксирован 0 или 1 раз равна

0.05^{10}+10\cdot 0.95\cdot 0.05^9=0.00000000001865234375

Тогда вероятность того, что неправильный ответ появится хотя бы 2 раза:

1-0.00000000001865234375=0.99999999998134765625  

Таким образом, можно сказать, что вероятность того, что детектор зафиксирует хотя бы 2 неправильных ответа, сильно близка к 1

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
yulya678 yulya678  06.09.2019 01:40
Цена шоколадной конфеты в 2 раза больше цены сливочное посадки. каких конфет можно купить больше и во сколько раз, заплатив при этом одинаковую сумму? как решить...
liiiiiiiiiii liiiiiiiiiii  06.09.2019 01:40
По 5 примеров горючих, трудногорючих и негорючих веществ...
maxirufer1 maxirufer1  06.09.2019 01:40
На отрезке ав длиной 15м отмечена точка с. найдите длины отрезков ас и вс,если : а)отрезок ас на 3м длиннее отрезка вс; б)отрезок ас в два раза длиннее отрезка вс;...
12363211 12363211  06.09.2019 01:40
Автотуристы были в пути в первый день 6: 00 а во второй 4: 00 сегодня проехали 1600 км какое расстояние проезжали туристы каждый день если они ехали с одинаковой...
samruk1974 samruk1974  06.09.2019 01:40
Решите ! 1)5-3x 11 2): a+3 a-3 36 6 - + ) : a-3 a+3 a^2-9 a-3...
Kosik1512 Kosik1512  06.09.2019 01:40
Совощной базы отправили в один магазин 270кг груш слив на 120 кг меньше чем груш яблок в 3 раза больше чем слив сколько всего кг фрукт в магазин...
aze1234 aze1234  06.09.2019 01:40
Вкоробці 11 олівців, із яких 6 червоні і 5 синіх. із коробки взяли 3 олівці. яка ймовірність того, що всі вони червоні?...
Александр3000 Александр3000  06.09.2019 01:40
Первая космическая скорость равна 8 м\с на этой скорости ракета может выйти на земную орбиту вычисли путь ракеты заполни таблицу и ответ на вопросы. скорость 8 км\с...
Lerochka0204 Lerochka0204  06.09.2019 01:40
Из каких этапов состоит работа над творческим проектом?...
peschanskaakris peschanskaakris  06.09.2019 01:40
Представьте данное произведение в виде произведения простых множителей. , ! 7) 37×1001; 8 )57×201; 9) 136×725; 10) 56×900....

Популярные вопросы