, ДАЮ. РЕШИТЬ МЕТОДОМ ИНТЕРВАЛОВ.
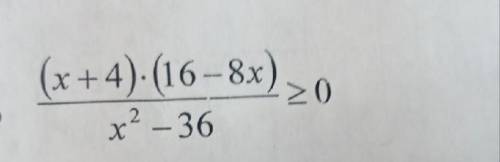
Другие вопросы по теме Математика
Популярные вопросы
- Разбери предложение по членам предложения. Над каждым словом обозначь...
3 - X 2. Дана функция: y = 2а)[ ) Определите область значений функции....
2 - Стороны трыкутныка доривнюють 8см 12 см и 14 см знайдить перымтр...
1 - Чому б я навчався в афінській (спартансьеій ) школіЧому б я навчався...
1 - Тжю қазақ әдебиеті 2 тоқсан сұсын өтірік зат жазбан мысалы: мен...
2 - Складіть таблицю розвиток середньовічних держав у Європі (форма...
1 - Напишите сочинение на казахском языке на тему озера Казахстана...
1 - докажи что треугольник ABC треугольнику MKC обязательные необходимо...
2 - Дана функция y=a−6. При каких значениях a значение функции равно...
3 - 4.Дополни предложения словами из рамки im, gibt, ist, und, Schulgebäude,...
3
х ∈ (-6;-4] ∪ [2;6)
Пошаговое объяснение:
ОДЗ:
1) Находим нули:
х₁=2, х₂=-4, х₃=6, х₄=-6
2) Отмечаем все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
3) Выясняем знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
4) Отмечаем знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.
5) После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «−», т.к. неравенство имеет вид
f (x) ≤ 0.
х ∈ [-6;-4] ∪ [2;6]