Даю 10000000000052-10000000000000 (52) . Задача на фото:

n = 3, n = -6

Пошаговое объяснение:

Квадратное уравнение имеет один корень, если его дискриминант равен нулю, т.е.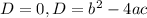

В этом уравнении: a = 3, b = -2n, c = -n + 6

Приравняем D к нулю:

По теореме Виета находим корни:

Проверка (необязательно):

при n = 3, уравнение имеет вид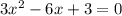 . Cокращаем на 3: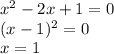

при n = -6, уравнение имеет вид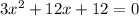 . Cокращаем на 3:

ответ: -6

Пошаговое объяснение: Это квадратное уравнение. Чтобы оно имело 1 корень, нужно, чтобы дискриминант был равен нулю.

D=(-2n)^2-4*3*(-n+6)=4n^2 +12n-72

4n^2+12n-72=0. Можно поделить на 4

n^2+3n-18=0

По теореме Виета n1=-6, n2=3. Поскольку нужно наименьшее значение, ответ -6