Даня задумал натуральное число, которое делится на би имеет ровно 6 делителей. Какое число мог задумать Даня? Укажите все возможные варианты.​

12, 18

Пошаговое объяснение:

Так как число делится на 6, в его разложении на простые множители должна входить хотя бы одна двойка и хотя бы одна тройка. Пусть число имеет вид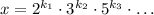 Тогда количество его делителей равно 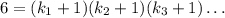Учитывая, что степени двойки и тройки не меньше 1, 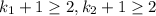. Если в числе есть хотя бы ещё один простой множитель, отличный от 2 и 3, то число делителей не меньше 2 * 2 * 2 = 8 > 6. Значит, число содержит только множители 2 и 3.

Так как 6 = 2 * 3, либо k₁ = 1, k₂ = 2, либо k₁ = 2, k₂ = 1. В первом случае x = 2·3² = 18, во втором — x = 2²·3 = 12.