1. Математика
  2. Даны векторы ab (3; -1; 2) и

Даны векторы ab (3; -1; 2) и bc (-2; 1; 1). расчет площади треугольника aвс​

KrIs1girl KrIs1girl    3   14.12.2019 21:20    0

Ответы
Mona228 Mona228  10.10.2020 20:37

AB(3-1;2)

BC(-2;1;1)

SABC = 1/2* |ABxBC| =

1/2 * √ ((-1-2)^2+(3+4)^2+(3-2)^2)=√59/2

ПОКАЗАТЬ ОТВЕТЫ
Karinago Karinago  10.10.2020 20:37

\frac{\sqrt{59} }{2}.

Пошаговое объяснение:

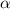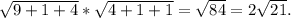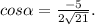Найдем угол \alpha между векторами. Скалярное произведение векторов равняется 3*(-2)+(-1)*1+2*1=-5. Произведение их модулей равняется \sqrt{9+1+4} *\sqrt{4+1+1}= \sqrt{84} =2\sqrt{21} .  Тогда cos\alpha =\frac{-5}{2\sqrt{21} } . Тогда, учитывая, что 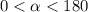0°, получаем 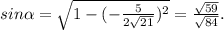sin\alpha =\sqrt{1-(-\frac{5}{2\sqrt{21} } )^2} =\frac{\sqrt{59} }{\sqrt{84} } . Найдём площадь как половину произведения сторон треугольника на синус угла между ними:

S=\frac{1}{2} \frac{\sqrt{59} }{\sqrt{84} } \sqrt{13} \sqrt{6} =\frac{\sqrt{59} }{2} .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
dashavr1 dashavr1  19.09.2019 20:50
2/12*16/14= кто знает как это решается?...
Kate110868 Kate110868  19.09.2019 20:50
Десятичная дробь.запись,чтение.сравнение десятичных дробей. обращение обыкновенной дроби в десятичную и наоборот. пример....
seregalock seregalock  19.09.2019 20:50
Найдите координаты середины c(x; y) отрезка ab...
anzhelikamilan anzhelikamilan  19.09.2019 20:50
Взяты образцы крови у жителей города n. вероятность обнаружить в крови свинец составляет 0,3. какова вероятность того, что у четверых из 10 человек тестирование, обнаружен в крови...
PoMOgiTe212lk PoMOgiTe212lk  19.09.2019 20:50
Решить премеры по матес 1 (158.368: 101+9412-2713)*(1372-63.567: 63) 2 87613+665760: 95+103*(500200-469937) и 3 1628*237+127608: (84928-84519) по действиям...
MrXMen MrXMen  19.09.2019 20:50
Детская площадка имеет форму прямоугольника, площадь которого равна 192м2. одна его сторона на 4 метров(-а) больше, чем другая. детской площадке необходимо построить бордюр. в магазине...
arsenal2108 arsenal2108  19.09.2019 20:50
Решите уравнение |2х-5|=9 |0.4x-1|=2.2 |2.5x-3|=7 |0.6+x|=7 |0.5x+3|=5 |0.2x+7|=8...
crosser001 crosser001  19.09.2019 20:50
Найдите объём прямоугольного параллелепипеда если его сторона равна 4 2/3 см,ширина 4/7см, высота 1,5 см...
ижепгпгаоуынсшыечто ижепгпгаоуынсшыечто  19.09.2019 20:50
Найдите : а) 3% от числа 120; б) 10% от числа 7; в) 25% от числа 200....
6ahah9812 6ahah9812  19.09.2019 20:50
Выполните действия: 1) 4,86÷(-1.8)-0,8•2,3+6; 2) 13,44÷(0,65-0,23•15); 3) 3,04÷(-1,6)+16,16÷16+7; 4) (99,99-6,54)÷(-62,3)•(-0,3)....

Популярные вопросы