Даны три последовательных натуральных числа. квадрат большего из них на 76 больше произведения двух других. найти среднее число.

101010101010101010101010101010100101101010101010101010

Даны три последовательных натуральных числа,  т.е. они образуют алгебраическую прогрессию с разностью на 1,  между элементами, положим что это алгебраическая прогрессия вида:

 , а разность между элементами

 Зная, что квадрат большего из них на 76 больше произведения двух других получаем:

 т.к.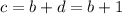 и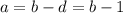

получаем:

 ответ: среднее число равно 25