1. Математика
  2. Даны точки м1(3; -1; 2) м2(4;

Даны точки м1(3; -1; 2) м2(4; -2; -1) составить уравнение плоскости проходящей через точку м1 перпендикулярно м1м2 и построить эту плоскость. 30

maga050508 maga050508    1   14.08.2019 21:40    0

Ответы
Kunpaw Kunpaw  20.08.2020 08:42

Координаты вектора M₁M₂ :

\overrightarrow{M_1M_2}=\{4-3;-2-(-1);-1-2\}=\{1;-1;-3\}

A(x-x_0)+B(y-y_0)+C(z-z_0)=0 - уравнение плоскости, проходящей через заданную точку, перпендикулярно вектору \overrightarrow{n}\{A;B;C\}

В нашем случае вектор нормали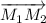 \overrightarrow{M_1M_2} и точка 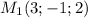M_1(3;-1;2). Подставляем их координаты, мы получим

1\cdot (x-3)-1\cdot(y+1)-3\cdot (z-2)=0\\ \\ x-3-y-1-3z+6=0\\ \\ x-y-3z+2=0

Последнее уравнение это искомое уравнение плоскости.


Даны точки м1(3; -1; 2) м2(4; -2; -1) составить уравнение плоскости проходящей через точку м1 перпен
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
kris0603 kris0603  09.07.2019 14:20
Девочка прочитала в 3 раза больше страниц чем ей осталось прочитать. известно также что она прочитала на 60 страниц больше чем осталось не прочитано. сколько страниц...
МиссисX2 МиссисX2  09.07.2019 14:20
Три сестры-таня,катя и валя-учатся в разных классах одной школы.таня старше кати,а катя старше вали.кто старше: таня или валя?...
likagluxova likagluxova  09.07.2019 14:20
Бельчонок пригласил в гости 12 своих лучших друзей. по случаю встречи все бельчата захотели обняться – каждая пара по одному разу. сколько было объятий?...
gjkbyf1984 gjkbyf1984  09.07.2019 14:20
в одному ящику залишилось 14кг яблук,а в другому на 9кг килограмив яблук залишилось у двох ящиках?...
ervinbek2005 ervinbek2005  09.07.2019 14:20
Студент обнаружил, что скорый поезд мимо неподвижного него за семь секунд, а мимо асфальтированной дорожки длиной 378 метров – за 25 секунд. чему равна длина поезда...
liza4608 liza4608  09.07.2019 14:20
Из двух зоопарков,находящихся друг от друга на расстоянии 168 км,сбежала мама слониха и её сын слонёнок.слониха бежит со скоростью 16км/ч, а слонёнок. бежит вдвое...
Odagio Odagio  09.07.2019 14:20
При пайке изделий из жести применяют сплав содержащий 2 части свинца и 5 частей олова сколько свинца и сколько олова содержит сплав массой 280 граммов...
Natalivizer Natalivizer  09.07.2019 14:20
8. запишите в семеричной системе счисления числа: 73; 14; 147....
noname0002 noname0002  09.07.2019 14:20
Нашли сумму 3 последовательных нечетных чисел,наименьшее из которых равно 1029....
iworld2rist iworld2rist  09.07.2019 14:20
Как найти общий наибольший делитель 72 и 385...

Популярные вопросы