Даны прямые вида у = kx+b. У первой прямой k=m, b=1, у второй k=1, b=т, у третьей k=0, b=3. Найдите все возможные значения m, такие, что
все три прямые пересекаются ровно в одной точке.
Другие вопросы по теме Математика
Популярные вопросы
- Почему союзники – шведские отряды оказались в итоге захватчиками земель?...
1 - Ион cl- имеет электронную конфигурацию...
2 - Нужно составить схему каждого предложения. чтобы хорошо учиться, надо быть хорошо...
2 - Услов названий женского рода с основой на шипящий звук в конце пишется ь знак...
3 - Как решить но 1пасике 56 ульев на другой 48 с первой пасике 80 кг б. мёда чем...
3 - Надо дописать эти предложения: 1.makes the same journey twice a year 2. desember-march:...
3 - Напишите сочинение рассуждение на тему , что такое доблесть )...
2 - Какой список называеться многоуровневым? проведите примеры...
2 - Разберите по членам предложения : здесь долгое время работали опытные оружейники....
2 - Как перевести смешанную дробь 3 целых 3/16 в десятичную?...
2
Пошаговое объяснение:
y₁=mx+1
y₂ = x+t
y₃ = 3
поскольку все прямые пересекаются в одной точке (хₙ; уₙ), для всех координаты этой точки пересечения будут (хₙ; 3), т.к. последняя прямая - это линия параллельная оси ох и координата уₙ =3
тогда просто найдем зависимость m от t
из уравнения первой прямой
mx+1 = 3 ⇒ x= 2/m
подставим этот х в уравнение второй прямой
x+t =3 2/m = 3-t ⇒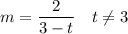
вот при всех таких m, вычисляемых в зависимости от t, при t≠ 3, прямые и будут пересекаться в одной точке