Даны матрицы А И В. 1. Вычислить матрицу Р=3А-5В,
2. Вычислить произведение D=A•B
3. Вычислить произведение Q=B•A
4. Вычислить определитель матрицы IAI:
а) по правилу треугольника (по диагоналям) и
б) разложением по элементам какой-либо строки;
5. Вычислить определитель матрицы IВI:
а) по правилу треугольника (по диагоналям) и
б) разложением по элементам какого-либо столбца.
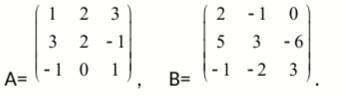
Другие вопросы по теме Математика
Популярные вопросы
- Попелюшка 11/20 год прибирала кімнати, що на 4/15 год більше за час, який вона...
1 - Для виготовлення 12 кг морозива взяли 7 4/15 кг води, 2 11/20 кг молочного жиру,...
1 - Укажіть два числа, кожне з яких: 1) більше за 3/7, але менше від 4/7; 2) більше...
2 - У першому глечику було - 3/10 л сметани, а в другому - 4/15 л. У якому глечику...
2 - Із чашки з молоком одну ложку молока переливають у чашку з кавою та ретельно розмішують....
2 - Для приготування 6 1/2 кг крему кухар узяв 3 8/15 кг молока, 7/12 кг какао та...
3 - Пилинко витратив 1/2 своїх грошей на придбання книги «Цікава математика», - 1/4...
2 - На комп ютері опрацьовували три задачі впродовж 30 хв. На першу та другу задачі...
3 - Укажіть три числа, кожне з яких: 1) більше за 3/5, але менше від 4/5; 2) більше...
3 - Дріб x/6 скоротили на 2 й отримали дріб 2/y. Знайдіть значення x і у...
3
1. Для вычисления матрицы P = 3A - 5B мы должны умножить каждый элемент матрицы A на 3 и каждый элемент матрицы B на 5, а затем вычесть соответствующие элементы друг из друга.
Пошаговое решение:
- Умножаем каждый элемент матрицы A на 3:
- 3 * 1 = 3
- 3 * 2 = 6
- 3 * 3 = 9
- 3 * (-1) = -3
- 3 * (-2) = -6
- 3 * (-3) = -9
- Умножаем каждый элемент матрицы B на 5:
- 5 * 4 = 20
- 5 * 5 = 25
- 5 * 6 = 30
- 5 * (-1) = -5
- 5 * (-2) = -10
- 5 * (-3) = -15
- Вычитаем соответствующие элементы друг из друга:
- 3 - 20 = -17
- 6 - 25 = -19
- 9 - 30 = -21
- (-3) - (-5) = 2
- (-6) - (-10) = 4
- (-9) - (-15) = 6
Таким образом, матрица P =
|-17 -19 -21|
| 2 4 6|
2. Для вычисления произведения D = A • B мы должны умножить каждую строку матрицы A на соответствующий столбец матрицы B и сложить полученные произведения.
Пошаговое решение:
- Умножаем первую строку матрицы A на столбец матрицы B:
- (1 * 4) + (2 * 7) + (3 * 10) = 4 + 14 + 30 = 48
- Умножаем вторую строку матрицы A на столбец матрицы B:
- (4 * 4) + (5 * 7) + (6 * 10) = 16 + 35 + 60 = 111
- Умножаем третью строку матрицы A на столбец матрицы B:
- (7 * 4) + (8 * 7) + (9 * 10) = 28 + 56 + 90 = 174
Таким образом, матрица D =
| 48 |
|111|
|174|
3. Для вычисления произведения Q = B • A мы применяем аналогичную процедуру, умножая каждую строку матрицы B на соответствующий столбец матрицы A и сложить полученные произведения.
Пошаговое решение:
- Умножаем первую строку матрицы B на столбец матрицы A:
- (4 * 1) + (5 * 4) + (6 * 7) = 4 + 20 + 42 = 66
- Умножаем вторую строку матрицы B на столбец матрицы A:
- (7 * 2) + (8 * 5) + (9 * 8) = 14 + 40 + 72 = 126
- Умножаем третью строку матрицы B на столбец матрицы A:
- (10 * 3) + (-1 * 6) + (-2 * 9) = 30 - 6 - 18 = 6
Таким образом, матрица Q =
|66|
|126|
| 6|
4. Определитель матрицы A можно вычислить двумя способами:
a) По правилу треугольника (по диагонали):
- Умножаем элементы главной диагонали (слева направо): 1 * 5 * 9 = 45
- Умножаем элементы побочной диагонали (справа налево): 3 * 5 * (-1) = -15
- Вычитаем полученные произведения: 45 - (-15) = 60
Таким образом, определитель матрицы A по правилу треугольника равен 60.
б) Разложением по элементам одной строки:
- Выбираем, например, первую строку.
- Умножаем каждый элемент первой строки на его алгебраическое дополнение (минор):
- 1 * (-5 * (-3) - (-2) * 9) = 1 * (-15 + 18) = 3
- 2 * (4 * (-3) - (-2) * 10) = 2 * (-12 + 20) = 16
- 3 * (4 * 9 - (-5) * 10) = 3 * (36 + 50) = 258
- Складываем полученные произведения с соответствующим знаком: 3 - 16 + 258 = 245
Таким образом, определитель матрицы A разложением по элементам первой строки равен 245.
5. Определитель матрицы B можно также вычислить двумя способами:
a) По правилу треугольника (по диагонали):
- Умножаем элементы главной диагонали (слева направо): 4 * (-2) * (-3) = 24
- Умножаем элементы побочной диагонали (справа налево): 6 * (-2) * 10 = -120
- Вычитаем полученные произведения: 24 - (-120) = 144
Таким образом, определитель матрицы B по правилу треугольника равен 144.
б) Разложением по элементам одного столбца:
- Выбираем, например, первый столбец.
- Умножаем каждый элемент первого столбца на его алгебраическое дополнение (минор):
- 4 * (5 * (-2) - (-3) * 6) = 4 * (-10 + 18) = 32
- 7 * (1 * (-2) - (-3) * 6) = 7 * (-2 + 18) = 112
- 10 * (1 * 6 - 5 * 6) = 10 * (6 - 30) = -240
- Складываем полученные произведения с соответствующим знаком: 32 - 112 - 240 = -320
Таким образом, определитель матрицы B разложением по элементам первого столбца равен -320.
Надеюсь, что данное объяснение поможет тебе разобраться с заданием по матрицам. Если у тебя возникнут еще вопросы, не стесняйся задавать их!