Даны координаты точек: А(1;-1;-4), B(-3;-1;0), C(-1;2;5), D(2;-3:1)
Тогда косинус угла между прямыми AB и CD равен
Другие вопросы по теме Математика
Популярные вопросы
- Как и почему изменялось положение кристьян во франции 12 14 веках...
3 - Представь себе что удалось услышать разговор с глобусом и чернильным...
3 - 5предложений про америку с переводом...
1 - Вкоробке 10 10 красных, 15 15 синих и 20 20 белых шариков. назовите наименьшее...
3 - Составь рассказ о продукции сельского хозяйства твоего края тверская...
2 - №1 выражение. а) m * 4,5 * 4 = б) -10 * а * 1,2 = в) х * (-2) * у * (-3,5)=...
2 - Воткрытом сосуде уровень жидкости понизился. если приток тепла к жидкости...
3 - Найди значения выражений 2,28+9,72: 12...
1 - Найдите значения выражения: a^2-9b^2/3ab: (1/3ab-1/a) при a=3 целых 1/7...
2 - Как в процессе испарения, если притока тепла к жидкости извне нет, меняется...
1
Пошаговое объяснение:
Для начала нужно найти прямые.
AB = B-A = (-3-1;-1-1;0+4) ; AB(-4;-2;4)
CD ищем по такому же принципу. Вычитаем координаты точек.
CD(3;-5;-4)
Считаем косинус. Формула косинуса равна: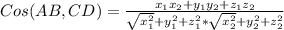
Считаем верхнюю часть. -4*3+-2*-5+4*-4 = -12+ 10 + -16 = -18, берём модуль. Это 18.
Считаем низ. 16 + 4 + 16 = 36, корень = 6; 3 + 25 + 16 = 44 корень из 44.
Следовательно в ответе - arccos 18/ (6корней из 44)