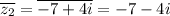Даны комплексные числа z1=-2i+3; z2= 4i-7. Выполнить: а) сложение, вычитание, умножение и деление этих чисел;
б) найти их модуль и сопряжённые им.
Другие вопросы по теме Математика
Популярные вопросы
- Сочинение по картине снегурочка ...
2 - Дано: BK биссектриса, угол ABC = 100° Найти: KC...
2 - 5 - тапсырма . Өлеңнен дисфемизмдерді теріп жазыңдар . Оларды...
3 - Какие числительные встречаются редко...
3 - 1. Промінь OK - бісектриса кута Вос. Знайдіть кут ВОС, якщо відомо,...
3 - Стр 308 глава 4-я письменно ответить на вопросы за ответ...
3 - Відношенням відрізків завдовжки aib називається...
2 - это сор надо вычеслить по теореме Виетта ...
3 - 4б) 1г нефти, попадая в водохранилище, покрывает тонким слоем...
2 - Исторические сведения о саках. Урок 3 Заполни пробелы. 1. По сведениям...
2
Пошаговое объяснение:
а)
б) Модуль комплексного числа a+bi можно найти по формуле
Сопряженным комплексному числу a+bi является число a-bi.
Тогда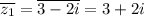 ,
,