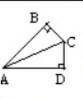
Даны два треугольника ABC,ABD(рис 1).Доказать ABC=ADC
Найти:угол BAD,если BC=CD,угол ACB=55°​

Чтобы доказать, что ∠ABC = ∠ADC, мы можем использовать два свойства треугольников:

1) Сумма углов в треугольнике равна 180°.
2) Если две стороны треугольника равны, то соответствующие углы при них тоже равны.

Для начала, нам нужно показать, что треугольники ABC и ADC равнобедренные, то есть имеют две равные стороны. Мы знаем, что BC = CD, и угол ACB = 55°.

1) Рассмотрим треугольник ABC. У него есть сторона AB и угол ACB. Мы можем найти третий угол треугольника, используя свойство суммы углов в треугольнике: угол ABC = 180° - угол BAC - угол ACB. Поскольку треугольник ABC является треугольником, сумма углов должна быть 180°, поэтому ∠ABC = 180° - ∠BAC - ∠ACB.

2) Рассмотрим треугольник ADC. У него есть сторона AD и угол ADC. Аналогично, мы можем найти третий угол треугольника, используя свойство суммы углов в треугольнике: угол ACD = 180° - угол CAD - угол ADC. Поскольку треугольник ADC является треугольником, сумма углов должна быть 180°, поэтому ∠ACD = 180° - ∠CAD - ∠ADC.

3) Так как мы знаем, что углы ACB и ACD равны, то ACB = ACD.

4) Теперь мы можем сравнить два треугольника ABC и ADC. У них есть равные стороны AB и AD, и равные углы ACB и ACD. Поэтому, по свойству "Если две стороны треугольника равны, то соответствующие углы при них тоже равны", получаем, что ∠ABC = ∠ADC.

Теперь, чтобы найти угол BAD, нам нужно воспользоваться свойством суммы углов в треугольнике. У нас уже есть угол ACB = 55°, и мы только что доказали, что ∠ABC = ∠ADC. Таким образом, угол ABD = 180° - ∠BAC - ∠ABC = 180° - ∠BAC - ∠ADC.