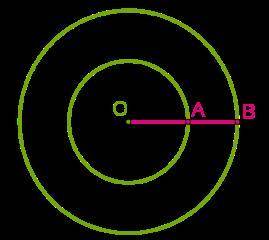
Даны два круга с общим центром O.

Rl_garums.png

Площадь меньшего круга равна 147см2. Отрезок AB = 4 см.
Значение числа π≈3.

Определи площадь большего круга.

Для решения этой задачи нам понадобятся формулы для нахождения площади круга и длины окружности.

Формула для площади круга:
S = π * r^2,
где S - площадь круга,
π - число пи (3,14),
r - радиус круга.

Формула для длины окружности:
C = 2 * π * r,
где C - длина окружности,
π - число пи (3,14),
r - радиус круга.

В данной задаче у нас есть два круга с общим центром O. Площадь меньшего круга равна 147 см^2. По условию, мы знаем, что AB = 4 см.

Чтобы найти площадь большего круга, нам нужно узнать его радиус. Для этого мы можем воспользоваться отрезком AB, так как он является диаметром меньшего круга.

Радиус меньшего круга равен половине диаметра (AB = 2r):
2r = AB = 4 см,
r = 4 см / 2 = 2 см.

Теперь, когда у нас есть радиус большего круга (2 см), мы можем найти его площадь, используя формулу:

S = π * r^2,
S = 3,14 * 2^2,
S = 3,14 * 4,
S = 12,56 см^2.

Таким образом, площадь большего круга равна 12,56 см^2.