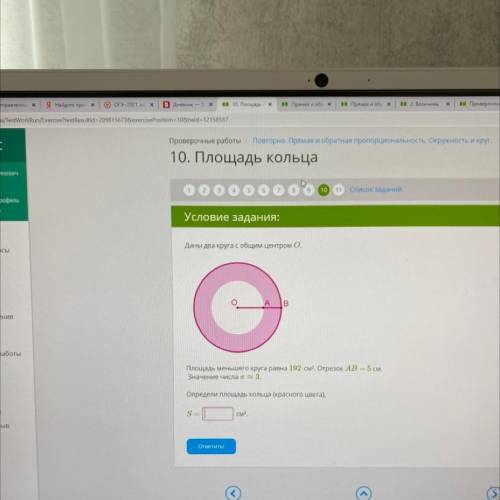
Даны два круга с общим центром О. А
В
Площадь меньшего круга равна 192 см. Отрезок AB = 5 см.
Значение числа п~ 3.
Определи площадь кольца (красного цвета).
S =
см?.
Другие вопросы по теме Математика
Популярные вопросы
- З наведених речень випишіть по кілька слів на кожен з принципів правопису....
2 - Розпишіть електронно-графічнв формули хімічних елементів з порядковими номерами...
1 - Подайте у вигляді добутку вираз ax + ny – az + nx + ay – nz...
1 - Знайти натуральни звязки неривности 5(x-2) 2x-2,2...
3 - Визначити, скільки односкладних речень ужито в наведеному нижче уривку з вірша...
2 - Висота правильної чотирикутної піраміди дорівнює 8 см а бічне ребро 10. Знайти...
2 - Найдите сторону а квадрата, если его площадь S равна: а) 64 Решение. Так как...
3 - paid payed pay to pay 2. Her parents aren t very strict. She out as late as...
1 - Сделайте все задания. в3 опишите картинку 1 где мальчик у компа...
2 - Охарактеризуйте спеціалізацію сільського господарства в нашому регіону (Херсон...
2
1. Начнем с определения площади круга (S1):
S1 = π * r1^2,
где π (пи) - это число, примерно равное 3.14,
а r1 - радиус меньшего круга.
2. Зная, что площадь меньшего круга равна 192 см^2, мы можем использовать это для вычисления радиуса:
192 = π * r1^2.
Для упрощения расчетов используем приближенное значение π = 3:
192 = 3 * r1^2.
Разделим обе стороны уравнения на 3:
r1^2 = 192 / 3 = 64.
Извлечем квадратный корень из обеих сторон:
r1 = √64 = 8.
3. Затем перейдем к площади кольца (S):
S = π * (r2^2 - r1^2),
где r2 - радиус большего круга.
4. Нам известно, что отрезок AB = 5 см.
Отсюда следует, что радиус большего круга (r2) равен r1 + AB:
r2 = r1 + 5 = 8 + 5 = 13.
5. Теперь, используя найденные значения радиусов, можем найти площадь кольца:
S = π * (r2^2 - r1^2) = 3 * (13^2 - 8^2) = 3 * (169 - 64) = 3 * 105 = 315.
Ответ: Площадь кольца (красного цвета) равна 315 см^2.