Даны числа z1=1+ 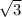
z2=0,5(Cos(-п/6) + I Sin (п/6)) представьте число z1 в тригонаметрической форме вычеслите записать в тригонаметрической форме
Другие вопросы по теме Математика
Популярные вопросы
- Зачем требуется два видока...
1 - СОСТАВИТЬ 6 ВОПРОСОВ К СОДЕРЖАНИЮ ТЕКСТА...
1 - Нужно составить план-конспект мообщения на тему Общая характеристика подцарства...
2 - Сор по информатике 4 класс 1 четверть...
1 - Определите степени окисления каждого элемента и выпишите формулы веществ окислителей...
1 - определить среднегодовую стоимость основных средств (ссг) и сумму амортизационных...
3 - Ergänzen Sie bitte die Tabelle. Необходимо заполнить таблицу склонением порядковых...
1 - Сочинение на тему о чем заставил меня задуматься рассказ изумруд...
3 - Как называется жанр . История - это история о событиях, которые произойдут...
1 - с химией. Напишите структурную формулу вещества С4Н8О, если известно, что оно...
1
Пошаговое объяснение:
Умножаем и числитель и знаменатель на число, сопряженное знаменателю, т.е на (1+i)
a=4·(1+i)/(1–i)·(1+i)=(4+4i)/(1–i2)=(4+4i)/(1–i2)=(4+4i)/2=2+2i – в алгебраической форме вида x+iy
при этом
x=2; y=2
см. переход от алгебраической к тригонометрической в приложении 1
|z|=√22+22=√8
tg φ =y/x=2/2=1 ⇒ φ =π/4
a=√8·(cos(π/4)+isin(π/4)) – в тригонометрической форме
2)
a2=(2+2i)2=4+8i+4i2=4+8i–4=8i
Запишем a2 в тригонометрической форме:
a2=8·(cos(π/2)+isin(π/2))
Решаем уравнение:
z3=8i
Извлекаем корень кубический . Применяем формулу
( см. приложение 2)
∛(8i)=∛8·(cosπ2+2πk3+isinπ2+2πk3), k ∈ Z
при k=0
первый корень
zo=2·(cosπ6+isinπ6)=3–√+i
при k=1
второй корень
z1=2·(cosπ2+2π3+isinπ2+2π3)=2⋅(cos5π6+isin5π6)=−3–√+i
при k=2
третий корень
z2=2·(cosπ2+4π3+isinπ2+4π3)=2⋅(cos3π2+isin3π2)=−i
Корни расположены на окружности радиуса 2
Точки zo;z1;z2 делят окружность на три ( потому что корень третьей степени) равные части, каждая по 120 °