Дано уравнение x/ x-3 - 2/ x+3 = 8/ x^2-9 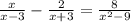А) Укажите область допустимых значений уравнения.
Б) Приведите рациональное уравнение к квадратному уравнению.
В) Найдите решение рационального уравнения.

Данное уравнение:

\(\frac{x}{x-3} - \frac{2}{x+3} = \frac{8}{x^{2}-9}\)

А) Область допустимых значений уравнения:

Первое условие для допустимых значений - знаменатели не должны быть равны нулю. Так как есть знаменатель \(x-3\) в первом слагаемом и знаменатель \(x+3\) во втором слагаемом, решим уравнение \(x-3=0\) и \(x+3=0\).

\(x-3=0 \Rightarrow x=3\)

\(x+3=0 \Rightarrow x=-3\)

Таким образом, область допустимых значений уравнения - все значения \(x\), кроме 3 и -3.

Б) Приведение рационального уравнения к квадратному уравнению:

Перенесем все слагаемые в левую часть уравнения:

\(\frac{x}{x-3} - \frac{2}{x+3} - \frac{8}{x^{2}-9} = 0\)

Для удобства приведем все слагаемые к общему знаменателю:

\(\frac{x(x+3) - 2(x-3) - 8}{(x-3)(x+3)} = 0\)

\(\frac{x^2 + 3x - 2x + 6 - 8}{(x-3)(x+3)} = 0\)

\(\frac{x^2 + x - 2}{(x-3)(x+3)} = 0\)

Раскроем скобки в знаменателе:

\(\frac{x^2 + x - 2}{x^2-9} = 0\)

C) Нахождение решения рационального уравнения:

Для нахождения решений уравнения \(x^2 + x - 2 = 0\), воспользуемся методами решения квадратных уравнений.

Разложим левую часть на множители:

\(x^2 + x - 2 = (x+2)(x-1) = 0\)

Таким образом, получаем два уравнения:

\(x+2 = 0\) и \(x-1 = 0\)

\(x+2 = 0 \Rightarrow x = -2\)

\(x-1 = 0 \Rightarrow x = 1\)

Проверим найденные значения в области допустимых значений:

Подставим \(x = -2\) и \(x = 1\) в исходное уравнение, чтобы убедиться, что они удовлетворяют ему:

При \(x=-2\): \(\frac{-2}{-2-3} - \frac{2}{-2+3} = 8/(-2^{2}-9)\)

При \(x=1\): \(\frac{1}{1-3} - \frac{2}{1+3} = 8/(1^{2}-9)\)

Оба значения подходят для исходного уравнения, так как знаменатели не равны нулю и не нарушается область допустимых значений.

Таким образом, решением рационального уравнения \(\frac{x}{x-3} - \frac{2}{x+3} = \frac{8}{x^{2}-9}\) являются \(x = -2\) и \(x = 1\), при условии что \(x\) не равно 3 и -3.