1. Математика
  2. Дано уравнение ||x*x-16|-7|-2а=0

Дано уравнение ||x*x-16|-7|-2а=0
найти сумму всех целых значений параметра , при которых уравнение имеет 8 решений.вопрос c1 рау

vanab322 vanab322    2   06.08.2019 09:08    0

Ответы
ak9512 ak9512  04.10.2020 00:48

||x^2-16|-7|-2a=0,\\||x^2-16|-7|=2a,\\\left \{ {{y=||x^2-16|-7|,} \atop {y=2a.}} \right.

Построим y=||x^2-16|-7|. (см. далее вложения)

1. Строим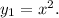 y_1 = x^2.

2. Строим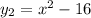 y_2 = x^2-16 путем смещения y₁ на 16 ед. вниз.

3. Строим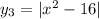 y_3 =|x^2-16| путем отражения части графика y₂, лежащей ниже Ox, относительно Ox.

4. Строим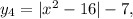 y_4 = |x^2-16|-7, путем смещения y₃ на 7 ед. вниз.

5. Строим y=||x^2-16|-7| путем отражения частей графика y₄, лежащих ниже Ox, относительно Ox.

Прямая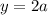 y = 2a будет пересекать наш график ровно в восьми точках, если 2a ∈ (0; 7), то есть при а ∈ (0; 3,5). Целые точки на этом интервале - {1; 2; 3}. Их сумма - 6.

ответ: 6.


Дано уравнение ||x*x-16|-7|-2а=0 найти сумму всех целых значений параметра , при которых уравнение
Дано уравнение ||x*x-16|-7|-2а=0 найти сумму всех целых значений параметра , при которых уравнение
Дано уравнение ||x*x-16|-7|-2а=0 найти сумму всех целых значений параметра , при которых уравнение
Дано уравнение ||x*x-16|-7|-2а=0 найти сумму всех целых значений параметра , при которых уравнение
Дано уравнение ||x*x-16|-7|-2а=0 найти сумму всех целых значений параметра , при которых уравнение
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
2346573920316 2346573920316  03.05.2021 10:55
Решите решите системы уравнений подстановки ​...
BroKeNxHeArT BroKeNxHeArT  03.05.2021 10:55
Как думаете, на каком фото стопы более широкие? У кого больше размер ноги? Слева или справа?...
Lina111334 Lina111334  03.05.2021 10:54
оформить как задачи)))напишите как надо записать в тетрадь полностью задачи ​...
mssinkevichna mssinkevichna  03.05.2021 10:54
2. [4] Автомобиль проехал 180 минут по шоссе со скоростью 100 км/ч, 2 часапо грунтовой дороге со скоростью 60 км/ч. Найти среднюю скорость автомобиля на всем пути.​...
karina847 karina847  03.05.2021 10:54
2. [4] Велосипедист проехал 240 минут со скоростью 15 км/ч и 4 часа со скоростью 10 км/ч. Найти среднюю скорость ДЕНКення велосипедиста на всех пути. 3. (2) Запишите формулу зависимости...
ninapopova197 ninapopova197  03.05.2021 10:54
Сор по математике четверть 4 5 класс​...
Liana03102000 Liana03102000  03.05.2021 10:53
На парковке стояли Форды, Мерседесы и прочие автомобили в количественном соотношении 8 : 7 :12 соответственно. После того как уехало четыре Форда и приехало несколько Мерседесов,...
hfdsgbgc hfdsgbgc  03.05.2021 10:52
57 чачтей все муку израсходвали .сколько кг муку остолась в пекарне​...
Alymov671 Alymov671  03.05.2021 10:52
. Пользуясь графиком движения всадника, определите: 1) Сколько часов всадник был в пути? 2) Какова продолжительность остановки? 3) Какова скорость движения всадника на обратном...
ulzhan16061999 ulzhan16061999  03.05.2021 10:52
Родители отправились в путешествие. Все вещи они упоковали в чемодан и в сумку Сумка с вещами весит 7кг. а в чемодане с вещами весит в 3раза больше Сколько всего кг весит сумка...

Популярные вопросы