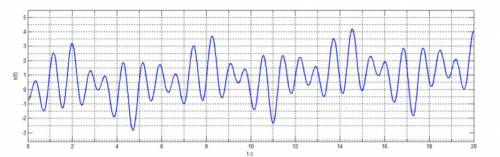
Дано уравнение сложного колебания, изображенного на рисунке. f(t)=0.08t+0.6sin(t)-0.3cos(2t)-0.3cos(3t)-0.1cos(4t)-0.2cos(5t)+0.9cos(6t)-1.4cos(8t)
Нарисуйте амплитудный спектр это сложного колебания.
Другие вопросы по теме Математика
Популярные вопросы
- России (особенно ядовитые! ) и многие ящерицы занесены в красную книгу. как...
2 - Решить ! 1)рюмин, разбирая печь в своем доме, доставшемся ему по наследству,...
2 - Язык. ! спишите вставляя пропущенные окончания. 1.солнце, светл.. и всплывает...
3 - Кобры растительноядные или плотоядные животные?...
2 - Средняя линия трапеции равна 65, а диагонали равны 50 и 120. найдите угол между...
3 - Жайғаным-түкті кілем, ілгенін-тықыр кілем. жауабын тауып бериниздерши...
3 - Как будет одним словом мясной отвар? ?...
2 - Из различных информационных источников подобрать несколько характерных примеров...
3 - 1. найдите диаметр и площадь круга, если его радиус равен 6 см. 2. найдите радиус...
3 - Решить .в треугольнике один из углов в два раза меньше и в три раза меньше двух...
2
Амплитудный спектр показывает, какие гармоники присутствуют в сложном колебании.
В данном случае, у нас есть следующие гармоники:
- Гармоника с основной частотой t, у которой амплитуда 0.08.
- Гармоника с частотой sin(t), у которой амплитуда 0.6.
- Гармоника с частотой cos(2t), у которой амплитуда -0.3.
- Гармоника с частотой cos(3t), у которой амплитуда -0.3.
- Гармоника с частотой cos(4t), у которой амплитуда -0.1.
- Гармоника с частотой cos(5t), у которой амплитуда -0.2.
- Гармоника с частотой cos(6t), у которой амплитуда 0.9.
- Гармоника с частотой cos(8t), у которой амплитуда -1.4.
Теперь нарисуем график амплитудного спектра, где по оси X будут отложены частоты, а по оси Y - амплитуды каждой гармоники.
Для этого создадим таблицу с двумя столбцами: "Частота" и "Амплитуда".
| Частота | Амплитуда |
|---------|-----------|
| t | 0.08 |
| sin(t) | 0.6 |
| cos(2t) | -0.3 |
| cos(3t) | -0.3 |
| cos(4t) | -0.1 |
| cos(5t) | -0.2 |
| cos(6t) | 0.9 |
| cos(8t) | -1.4 |
Теперь можем построить график, отмечая на оси X соответствующие частоты, а на оси Y - амплитуды каждой гармоники.
График будет иметь вид с дискретными точками, так как у нас есть конкретные значения амплитуд каждой гармоники.
После построения графика, мы увидим, какие гармоники присутствуют в данном сложном колебании и какова их амплитуда.
Например, первая точка на графике будет находиться на частоте t и иметь высоту 0.08. И так далее.
Надеюсь, этот ответ будет понятен для школьника и поможет ему понять, как нарисовать амплитудный спектр сложного колебания, используя данное уравнение.