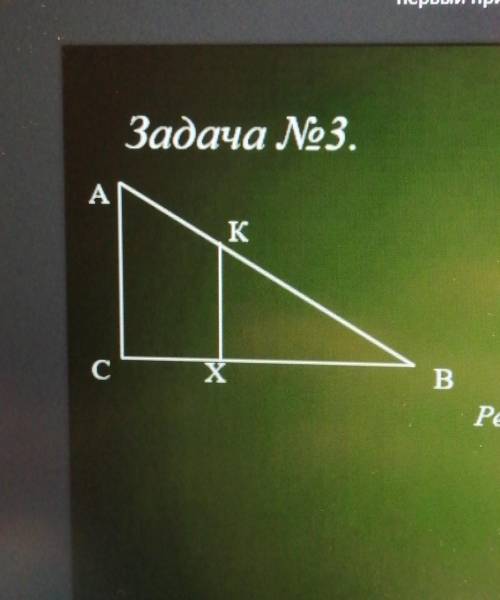
Дано: тр. АВС, угол C=90°
KX пенпендикулярно CB, K относится к АB,X относится к CB
KY=5,1 см, АС=15,3 см , CB=60 см
Найти: ХВ
​

Для решения задачи нам необходимо применить теорему Пифагора и соотношение между подобными треугольниками.

1. Так как угол C равен 90 градусам, треугольник ABC является прямоугольным, а сторона CB является гипотенузой.

2. Используя теорему Пифагора, мы можем найти длину стороны AB:
AB^2 = AC^2 + CB^2
AB^2 = (15.3 cm)^2 + (60 cm)^2
AB^2 = 234.09 cm^2 + 3600 cm^2
AB^2 = 3834.09 cm^2
AB ≈ 61.97 cm

3. После этого, мы можем использовать соотношение между подобными треугольниками для нахождения длины отрезка XB:
AB/XB = CB/YK
XB = (AB * YK) / CB
XB = (61.97 cm * 5.1 cm) / 60 cm
XB ≈ 5.3585 cm

Таким образом, длина отрезка XB около 5.36 см.