Дано точки А( - 2; 1; 3), В(3; - 2; -1) і С( - 3; 4; 2). Знайдіть: 1) Координати векторів ;
2) Модуль вектора ;
3) Координати вектора .

1) Координаты вектора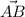 находятся вычитанием из координат конечной точки 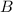соответствующие координаты начальной точки . То есть,

{ } = { } ;

{ } = { } ;

{ } = { };

{ } = { };

{ } = { };

{ } = { };

2) Модуль вектора находится как квадратный корень из суммы квадратов координат вектора. То есть,