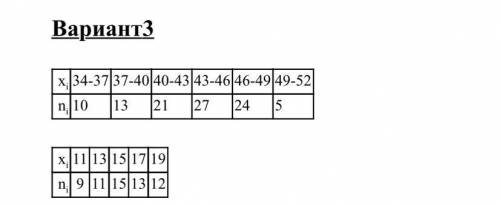
Дано распределение признака Х (случайной величины Х), полученной по n наблюдениям. Необходимо: 1) построить полигон, гистограмму, кумуляту и эмпирическую функцию;
2) найти: а) среднюю арифметическую;
б) медиану и моду;
в) дисперсию и среднее квадратическое отклонение;
г) вариационный размах и коэффициент вариации.
нужно
Другие вопросы по теме Математика
Популярные вопросы
- Сообщение об население и культуры австролии...
2 - Выразите в более мелких мерах: 5 м 17 см 4 м 55 см 3 р.2 к. 6 р.85 к. 3 кг...
1 - Предложение tom (to swim) in the sea во всех временах...
3 - Хто був сучасником п.полуботка? і.мазепа , п.орлик , петро 1 , б. хмельницький...
2 - 25 : сочинение на тему поход в театр сказка о царе салтане...
3 - 1.с какими из перечисленных стран граничит северо-западный район а) польша...
1 - Что вы думаете о том, кто такие пчелы и какое отношение они имеют к бабочками?...
3 - Охарактеризувати героїв з твору митькозавр із юрківки...
2 - Ямог бы просто плыть по (сочинение-монолог по рассказу э.хемингуэя )....
3 - Опишите внешний вид магнатов вкл и польши....
3
1) Построение полигона, гистограммы, кумуляты и эмпирической функции:
- Для построения полигона нужно построить столбчатую диаграмму, где по оси X будет откладываться значение признака Х, а по оси Y - частота встречаемости этого значения. Затем соединим вершины столбцов ломаной линией.
- Для построения гистограммы возьмем столбчатую диаграмму, но в этом случае ширина каждого столбца будет пропорциональна интервалу, в котором находится значение признака Х.
- Для построения кумуляты нужно просто построить ломаную линию, соединяющую точки с координатами (значение признака Х, накопленная частота встречаемости).
- Для построения эмпирической функции нужно отложить по оси X значения признака Х в порядке возрастания, а по оси Y - накопленную частоту встречаемости. Затем соединим точки ломаной линией.
2) Вычисление средней арифметической:
- Чтобы найти среднюю арифметическую, нужно сложить все значения признака Х и разделить полученную сумму на общее количество наблюдений (n).
3) Нахождение медианы и моды:
- Чтобы найти медиану, нужно упорядочить значения признака Х по возрастанию и выбрать среднее значение (если n - нечётное) или среднее арифметическое двух средних значений (если n - чётное).
- Для нахождения моды нужно найти значение признака Х, которое встречается чаще всех остальных значений.
4) Вычисление дисперсии и среднего квадратического отклонения:
- Для нахождения дисперсии нужно вычислить среднее арифметическое квадратов отклонений каждого значения признака Х от средней арифметической.
- Среднее квадратическое отклонение - это квадратный корень из дисперсии.
5) Вычисление вариационного размаха и коэффициента вариации:
- Вариационный размах это разность максимального и минимального значений признака Х.
- Коэффициент вариации равен отношению среднего квадратического отклонения к средней арифметической.
Надеюсь, я смог объяснить задачу достаточно ясно и подробно, чтобы ты понял. Если у тебя возникнут еще вопросы, не стесняйся задавать!