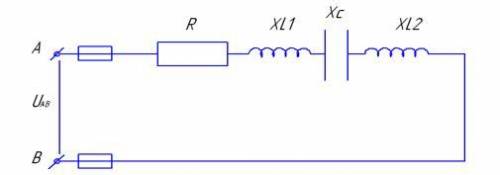
Дано: R1 = 16 oм
R2 = - ом
Xl1 = 10 oм
XL2 = 8 ом
Xc1 = 6 om
Xc2 = - om
U = 80
Найти:
1) полное сопротивление Z;
2) напряжение, U приложенное к цепи ;
3) ток ;
3) угол сдвига фаз φ; ( по величине к знаку)
4) активную P, реактивную Q и полную S мощности цепи.
Начертить в маштабе векторную диаграмму цепи и пояснить ее построение.

Чтобы решить данный вопрос, мы будем использовать формулу для нахождения полного сопротивления и формулу для нахождения тока.

1) Полное сопротивление (Z) состоит из активного и реактивного сопротивлений и вычисляется по формуле:
Z = R + jX,
где R - активное сопротивление, X - реактивное сопротивление.

В данном случае, активное сопротивление (R) равно сумме R1 и R2:
R = R1 + R2 = 16 - ом

Реактивное сопротивление (X) состоит из индуктивной (Xl) и ёмкостной (Xc) реактивностей:
X = Xl1 + Xl2 + Xc1 + Xc2 = 10 + 8 + 6 - ом

Таким образом, полное сопротивление Z:
Z = R + jX = 16 - ом + j(10 + 8 + 6) - ом = 16 - ом + j24 - ом = 16 + j24 - ом

2) Напряжение, U, приложенное к цепи, равно заданному значению:
U = 80 - В

3) Ток (I) можно найти, используя формулу Ohm's Law:
I = U / Z,
где U - напряжение, Z - полное сопротивление.

Подставляя известные значения, получаем:
I = 80 / (16 + j24) - А

4) Угол сдвига фаз (φ) можно найти, используя тангенс:
φ = arctan(X / R),
где X - реактивное сопротивление, R - активное сопротивление.

Подставляя известные значения, получаем:
φ = arctan((10 + 8 + 6) / 16) - рад

5) Активная мощность (P) вычисляется по формуле:
P = U * I * cos(φ),
где U - напряжение, I - ток, φ - угол сдвига фаз.

Подставляя известные значения, получаем:
P = 80 * (80 / (16 + j24)) * cos(arctan((10 + 8 + 6) / 16)) - Вт

6) Реактивная мощность (Q) вычисляется по формуле:
Q = U * I * sin(φ),
где U - напряжение, I - ток, φ - угол сдвига фаз.

Подставляя известные значения, получаем:
Q = 80 * (80 / (16 + j24)) * sin(arctan((10 + 8 + 6) / 16)) - Вар

7) Полная мощность (S) вычисляется по формуле:
S = U * I,
где U - напряжение, I - ток.

Подставляя известные значения, получаем:
S = 80 * (80 / (16 + j24)) - ВА

Чтобы построить векторную диаграмму цепи, мы будем использовать комплексные числа и их геометрическую интерпретацию. Каждый компонент сопротивления будет представляться вектором на комплексной плоскости, где активное сопротивление (R) будет представлено по оси абсцисс (действительная ось), а реактивное сопротивление (X) - по оси ординат (мнимая ось).

Для построения вектора полного сопротивления (Z), мы рисуем вектор от начала координат до точки (16, 24) на комплексной плоскости.

Для построения вектора напряжения (U), мы рисуем вектор от начала координат до точки (80, 0) на комплексной плоскости.

Для построения вектора тока (I), мы рисуем вектор от начала координат до точки, которая находится на пересечении векторов полного сопротивления (Z) и напряжения (U) на комплексной плоскости.

Для нахождения угла сдвига фаз (φ), мы используем геометрическую интерпретацию тангенса. Вектор тока (I) и вектор полного сопротивления (Z) образуют прямоугольный треугольник на комплексной плоскости. Угол, образованный между горизонтальной осью и вектором тока (I), является углом сдвига фаз (φ).

Рисуем векторы на комплексной плоскости, обозначаем угол сдвига фаз (φ) и масштабируем оси для отображения всех векторов. Ось абсцисс (действительная ось) будет отображать значение активной мощности (P), а ось ординат (мнимая ось) - значение реактивной мощности (Q).

Объясняем построение векторной диаграммы школьнику, указывая на каждый вектор и его значение, объясняя измерения на оси и значение угла сдвига фаз.

Это подробное решение позволит школьнику понять пошаговый процесс решения задачи и построения векторной диаграммы для данной электрической цепи.