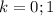Дано комплексное число z = 3/2 - sqrt(3)/2*i 1) найти z + z(с чертой над z) , z * z(с чертой над z), z/z(с чертой над z). 2) записать z в тригонометрической форме, вычислить z^4, и корень квадратный в 4й степени z
Другие вопросы по теме Математика
Популярные вопросы
- ОЧЕНЬ НУЖНО. З точки В яка розміщена на відстані 1 см від площини, проведено дві...
2 - Площа кільця, утвореного двома концентричними колами, дорівнює 25π см2. Знайдіть...
3 - Ортогональной проекцией треугольникас площадью 48 см2 является треугольник со сторонами...
2 - Заполни пропуски нужной формой глагола “to be” в отрицательных (-) и во предложениях....
2 - Запишіть хронологічний ланцюжок утворення Закарпатської області у складі УРСР (...
3 - 1.Почему после убийства Цезаря в Римском государстве вспыхнула гражданская война?...
3 - 1. Реши задачу.В столовую привезли 40 банок огурцов по 5 кг в каждой и 50 банокогурцов...
3 - Какие нравственные проблемы поднимает писатель в рассказах « Кукла», «Живое пламя»...
1 - Повторите правило образования времени. Раскройте скобки, ответы запишите в тетрадь....
3 - Що втратила Зграя, вигравши Джонатана?...
2
Дано комплексное число в алгебраической форм:
в алгебраической форм:
где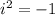 по определению
по определению
Тогда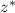 комплексно-сопряженное числу комплексному числу
комплексно-сопряженное числу комплексному числу  :
:
(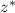 то же что у вас z с чертой!)
то же что у вас z с чертой!)
а)
б) Запишем наше комплексное число в тригонометрической форме:
в тригонометрической форме:
где модуль комплексного числа
модуль комплексного числа 
В нашем случае
Итак, число в тригонометрической форме с учетом (1) и (2):
в тригонометрической форме с учетом (1) и (2):
Для нахождения четвертой степени числа применим формулу Муавра при
применим формулу Муавра при 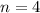 :
:
Известно, что корень n-й степени из комплексного значения имеет n различных значений. В нашем случае нужно найти корень 2-й степени, а значит корень 2-й принимает два различных значения.
при