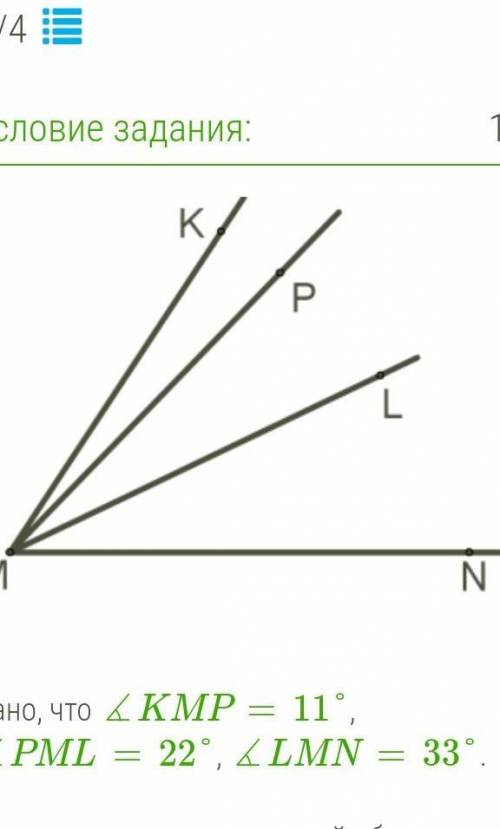
Дано, что ∡KMP=11°, ∡PML=22°, ∡LMN=33°. Сколько углов во внутренней области угла ∡KMN с разными градусными мерами, включая сам угол ∡KMN?
​

Ffffjkjkkejkwke hzjsjaj jajakkz jjjs

Для решения данной задачи, нам необходимо вычислить меру угла ∡KMN. Меру этого угла можно найти, используя свойства углов, образованных секущей и касательной к окружности.

Из данного изображения видно, что угол ∡KMN является внутренним областью угла ∡LMN. Мы знаем, что мера угла ∡LMN равна 33°.

Также известно, что ∡PML - это половина угла ∡KMN. Мера угла ∡PML составляет 22°. Половину этого угла можно получить, разделив его меру на 2: 22° / 2 = 11°.

Теперь у нас есть два известных угла: ∡KMP = 11° и ∡LMN = 33°. Мы можем использовать эти углы, чтобы найти меру угла ∡KMN.

Так как углы на смежных сторонах касательной и секущей окружности находятся в соотношении 1:1, мы можем записать уравнение:
∡KMP + ∡LMN + ∡KMN = 180°.

Заменяем известные значения:
11° + 33° + ∡KMN = 180°.

Вычитаем из обоих сторон уравнения известные значения:
44° + ∡KMN = 180°.

Вычитаем 44° из обоих сторон уравнения:
∡KMN = 180° - 44°.

Вычисляем:
∡KMN = 136°.

Таким образом, мера угла ∡KMN равна 136°.

Теперь, чтобы найти количество углов во внутренней области угла ∡KMN с разными градусными мерами, мы можем просмотреть все возможные градусные меры меньше 136°.

- Угол ∡KMN: 136° (сам угол)
- Угол ∡KNM: как известно, ∡KMN = ∡KNM, таким образом мера этого угла также равна 136°.
- Угол ∡KML: ∡KMN + ∡LMN = 136° + 33° = 169°.
- Угол ∡KMP: дано, что мера этого угла равна 11°.

Таким образом, во внутренней области угла ∡KMN есть 4 угла с разными градусными мерами:

1) ∡KMN = 136°
2) ∡KNM = 136°
3) ∡KML = 169°
4) ∡KMP = 11°.