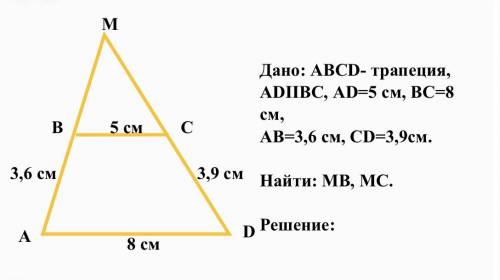
Дано: АВСD- трапеция, АDIIВС, АD=5 см, ВС=8 см,
АВ=3,6 см, СD=3,9см.
Найти: МВ, МС.
Решение:
Другие вопросы по теме Математика
Популярные вопросы
- Найдите неопределенный интеграл от функции....
1 - Скласти враження про твір Останній листок...
1 - У чому полягав новий сенс життя, відкритий християнами?...
1 - Письмо. Перепишите текст, вставляя нужные буквы и раскрывая скобки. Выполните...
2 - Исключи из предложенного списка лишнее слово: Панкреатиты, гастрит, цирроз печени,...
1 - даю все, Қазақ тілі 4 тоқсан ТЖБ, Onlinemektep. net...
1 - Что вы узнали о Снегурочке из данного эпизода? Дайте развернутый ответ с примерами...
2 - 1 Match to make up the names of famous landmarks in Kyiv.Number the pictures.1...
2 - Виберіть відділ рослин, якому характерний опис: рослини мають вегетативні та...
2 - Знайдіть суму коренів рівнянь: 5 х + 10 = 15 х + 40 і 2 ( –5 х+ 10) = 80...
1
6 см; 6,5 см
Пошаговое объяснение:
ΔАМD подобен ΔВМС (∠МВС=∠МАD, ∠М - общий)
Пусть ВМ=х см, тогда АМ=3,6+х см.
АD/BC=АМ/МВ; 8/5=(3,6+х)/х
8х=5(3,6+х); 8х=18+5х; 3х=18; х=6. МВ=6 см.
Пусть МС=у см, тогда МD=3,9+у см.
АD/ВС=(3,9+у)/у; 8у=5(3,9+у); 8у=19,5+5у; 3у=19,5; у=6,5. МС=6,5 см.