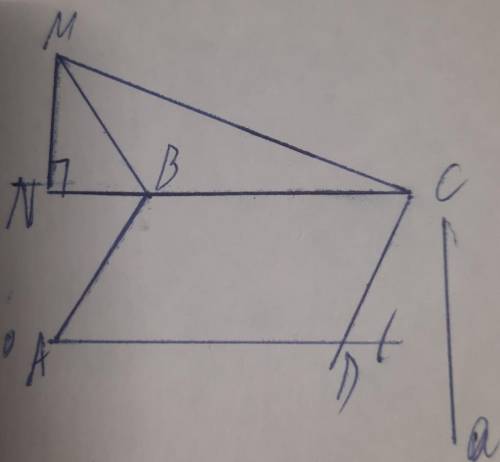
Дано: Авсд-параллелограмм
ВМС-тупоугольный
М∉(АВС)
MN перпендикулярен BC
a||MN
Док-ть
а пересекает (АВС)​

Дана геометрическая фигура, которая представляет собой параллелограмм АВС и треугольник ВМС. Требуется доказать, что прямая "а" пересекает окружность, описанную вокруг параллелограмма АВС (обозначенную (АВС)).

Для начала, рассмотрим данные:

1. АВС - параллелограмм: это означает, что противоположные стороны параллелограмма параллельны. В данном случае, сторона АВ и сторона СD будут параллельны.

2. ВМС - тупоугольный треугольник: это означает, что угол МВС больше 90 градусов.

3. М∉(АВС) - точка М не принадлежит окружности, описанной вокруг параллелограмма АВС: это означает, что точка M находится вне этой окружности.

4. MN перпендикулярен BC: это означает, что прямая MN образует прямой угол с отрезком BC.

5. a || MN: это означает, что прямая a параллельна прямой MN.

Теперь, для доказательства того, что прямая a пересекает окружность (АВС), мы можем использовать следующий алгоритм:

Шаг 1: Используя данные о параллельности прямых MN и a, мы можем сделать вывод, что прямые MN и a также параллельны стороне АВ параллелограмма АВС. Это связано с тем, что a || MN и MN перпендикулярна стороне BC, а по свойству параллелограмма противоположные стороны параллельны.

Шаг 2: В связи с тем, что прямые a и MN параллельны стороне АВ, они также параллельны и стороне СD параллелограмма, так как сторона СD также параллельна стороне АВ.

Шаг 3: Так как MN перпендикулярна стороне BC и a || MN, а, следовательно, параллельна стороне СD, мы можем сделать вывод, что прямая a также перпендикулярна стороне ВM треугольника ВМС.

Шаг 4: Так как прямая а перпендикулярна стороне ВM треугольника ВМС, мы можем сделать вывод, что прямая а также перпендикулярна стороне ВС параллелограмма.

Шаг 5: В связи с тем, что прямая а перпендикулярна стороне ВС и параллельна стороне АВ, мы можем сделать вывод, что прямая а также перпендикулярна стороне АВ параллелограмма АВС.

Шаг 6: Из шага 5 следует, что прямая а перпендикулярна и сторонам АВ и СD, то есть она пересекает сторону СD параллелограмма АВС.

Шаг 7: Так как прямая а пересекает сторону СD параллелограмма, которая является хордой окружности (АВС), мы можем сделать вывод, что она также пересекает окружность (АВС).

Таким образом, мы доказали, что прямая а пересекает окружность, описанную вокруг параллелограмма АВС.