Дано:
∆АВС.
АС||МN.
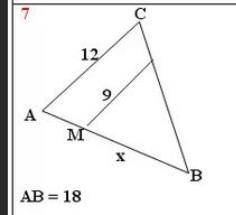
АВ=18см.
МN=9см.
АС=12см.
Найти: МВ-?

Для решения этой задачи, нам понадобится использовать основные свойства параллельных прямых и равных треугольников.

1. Из условия задачи следует, что МN || AC. Вспомним свойство: если две прямые параллельны, то соответственные углы равны. Значит, углы CAN и MNB равны между собой.

2. Также из дано следует, что треугольник ABC равнобедренный (AB = AC), поэтому угол BAC равен углу BCA. Так как углы CAN и MNB равны, то углы MNA и MBA равны между собой.

3. Обратите внимание на стороны треугольника ABC. У нас даны стороны AB = 18 см и AC = 12 см. Так как AB = AC, то треугольник ABC равнобедренный, а значит сторона BC равна стороне AB или AC. Поэтому BC = 18 см.

4. Используем свойство равных треугольников: если у двух треугольников равны соответствующие углы и одна сторона одного треугольника равна соответствующей стороне другого треугольника, то эти треугольники равны.

Рассмотрим треугольники BCN и MBA:

- У них равны углы MNA (из пункта 2) и NMC (как вертикальные углы).
- У них равны стороны MN = 9 см (из дано) и NM (которая равна MC по свойству равных сторон).

Поэтому треугольники BCN и MBA равны.

5. Следовательно, сторона BN равна стороне BA, то есть BN = 18 см.

6. Зная, что BC = 18 см и BN = 18 см, мы можем вычислить MB, применяя свойство треугольника: сумма длин двух сторон всегда больше третьей стороны.

MB < BC + BN
MB < 18 + 18
MB < 36

Таким образом, МВ меньше 36 см.

Ответ: МВ < 36 см.