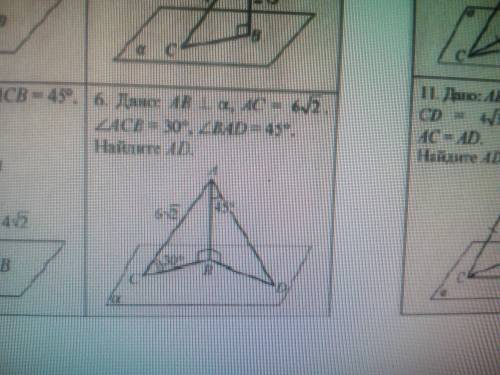
Дано: АВ перпендикулярно плоскости α ,АС=6√2, ∠АСВ=30°,∠ВАD=45°. Найти : АD.

Чтобы найти значение АD, мы можем использовать свойства треугольника и треугольника с прямым углом.

1. Известно, что треугольник ВАС - прямоугольный треугольник, поскольку АВ перпендикулярно плоскости α.

2. Также известны два угла внутри этого треугольника: ∠АСВ = 30° и ∠ВАD = 45°.

3. Мы можем использовать свойство суммы углов в треугольнике, чтобы найти третий угол треугольника ВАС:
∠САВ + ∠АСВ + ∠ВАС = 180°.
∠САВ + 30° + 90° = 180°.
∠САВ = 180° - 30° - 90° = 60°.

4. Так как у нас есть значение угла АСВ (30°), мы можем использовать свойства треугольника, чтобы найти отношение сторон в этом треугольнике:
ВА/АС = sin(∠АСВ).
ВА/6√2 = sin(30°).
ВА/6√2 = 1/2.
ВА = 6√2 * 1/2.
ВА = 3√2.

5. Мы можем использовать свойства треугольника с прямым углом, чтобы найти значение стороны АD:
ВА/АС = tan(∠ВАД).
3√2/6√2 = tan(45°).
1/2 = tan(45°).

Таким образом, АD = АС = 6√2.

Ответ: АD = 6√2.