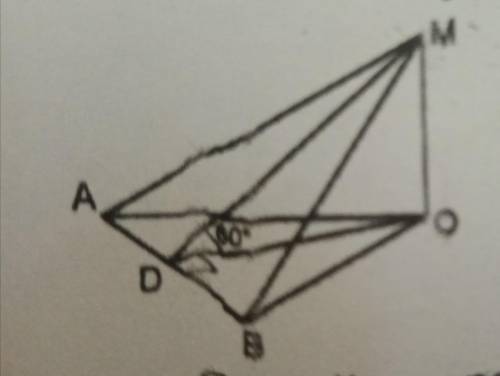
Дано: АВ =14, ОВ=15, АО= 13 найти Samb
Другие вопросы по теме Математика
Популярные вопросы
- Катастрофа відрізняється від аварії: А) наявністю людських жертв;Б)...
1 - 10.В результате издания указа о «вольных хлебопашцах»: а) барщина...
2 - сделать сравнительную таблицу, гражданские и трудовые правоотношения...
1 - решить задачки по геометрии,а то я уже 4 час сижу не могу их сделать.вы...
2 - Какие образовательные учреждения стали массово открываться в Советской...
1 - Определите стиль и тип текста. Реши орфографические и пунктуационные...
3 - Який напрямок мають серединно-океанічні хребети?...
1 - БИОЛОГИЯЯ 21. До форм безкисневого розщеплення глюкози належать:...
2 - Установите соответствие между функциями и их графиками....
2 - У МЕНЯ 7 МИН ДО СДАЧИ УЧИТЕЛЮ ДАЮ 15 Б написать 5 предложений с...
3
от А да О потом О В В М М Д
Пошаговое объяснение:
Таким образом, по теореме Пифагора, можно записать следующее уравнение для треугольника АОВ:
АО² + ОВ² = АВ²
Подставляем известные значения:
13² + 15² = 14²
169 + 225 = 196
394 = 196
Так как уравнение не выполняется, можно сделать вывод, что треугольник АОВ не является прямоугольным.
Следовательно, мы не можем использовать теорему Пифагора для нахождения Samb.
Для решения этой задачи, мы можем использовать формулу площади треугольника по трём сторонам - формула Герона.
Формула Герона позволяет нам найти площадь треугольника, зная длины его сторон.
Сначала нужно найти полупериметр треугольника, который вычисляется по формуле:
p = (АВ + АО + ОВ) / 2
p = (14 + 13 + 15) / 2
p = 42 / 2
p = 21
После нахождения полупериметра, мы можем найти площадь треугольника по формуле Герона:
Samb = √(p * (p - АВ) * (p - АО) * (p - ОВ))
Samb = √(21 * (21 - 14) * (21 - 13) * (21 - 15))
Samb = √(21 * 7 * 8 * 6)
Samb = √(7056)
Samb ≈ 83.92
Таким образом, площадь треугольника АмВ составляет примерно 83.92 квадратных единиц.