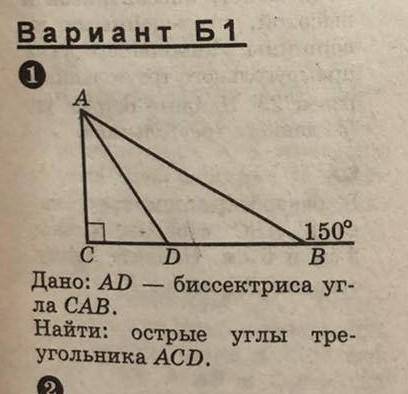
Дано: AD - биссектриса угла САВ, Найти: острые углы тре
угольника АCD.​

Чтобы найти острые углы треугольника ACD, нам нужно использовать свойство биссектрисы, которое гласит, что биссектриса угла делит его на два равных угла.

Итак, у нас есть биссектриса AD, которая делит угол CAD на два равных угла (назовем их угол MAD и угол DAC).

Поскольку угол MAD и угол DAC равны, мы можем записать следующее:

Угол MAD = Угол DAC = x

Теперь нам нужно найти острый угол треугольника ACD. Для этого мы будем использовать свойство суммы углов треугольника, которое гласит, что сумма углов треугольника равна 180 градусам.

Треугольник ACD имеет три угла: угол CAD, угол DAC и угол ACD.

Сумма углов треугольника равна:

Угол CAD + Угол DAC + Угол ACD = 180 градусов

Мы уже знаем, что Угол CAD = 2x и Угол DAC = x. Подставив эти значения в уравнение, мы получаем:

2x + x + Угол ACD = 180 градусов

3x + Угол ACD = 180 градусов

Теперь нам нужно найти Угол ACD. Для этого мы выразим его через x:

Угол ACD = 180 градусов - 3x

Итак, мы получили выражение для острого угла треугольника ACD через x. Для того чтобы найти его конкретное значение, нам нужна дополнительная информация о величине угла MAD.

Если у нас будет такая информация, мы сможем заменить значение угла MAD в выражении и найти острый угол треугольника ACD. Без дополнительных данных нам не удастся найти точное значение острого угла треугольника ACD.