Дано ABC,угол B = 90 гр
BH перпендикулярно AC,AB = 20, HC=30
Найти BH
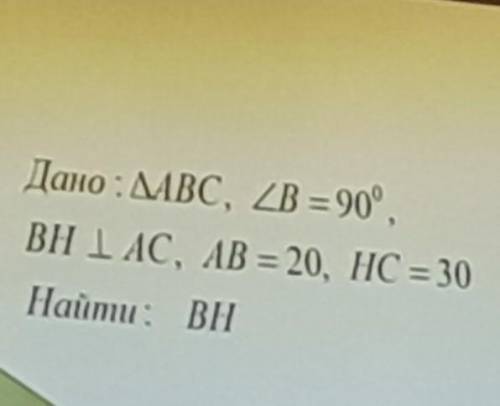
Другие вопросы по теме Математика
Популярные вопросы
- Ткани из этого волокна при намокании теряют прочность. Какое...
2 - Сколько вещества получит больной, если дават ему на прием 5,10...
3 - Чому в Англії не прийняли цивільний кодекс?...
2 - Електрон знаходиться у однорідному електричному полі з напруженістю...
1 - 5. Интенсивный переход жидкости в пар, происходящий с образованием...
2 - Жүсіп баласұғынның ұлтты кім?...
3 - Тау созине 4 5 соз жазып беринызшы отиниш...
2 - Является ли число 4 корнем уровнения ?И ещё 1Найти значение...
1 - Папа поймал 16 окуней а щук в 4 раза меньше. Сколько всего рыб...
2 - Чье имя Самир (какой национальности)? Узбекское, лезгинское,...
2
В данном случае, гипотенуза треугольника ABC - это отрезок AC, а катеты - отрезки AB и HC.
Для начала, мы знаем, что гипотенуза AC равна 50 (AB + HC).
Теперь, мы можем использовать теорему Пифагора, чтобы найти длину отрезка BH:
BH^2 = AC^2 - AB^2
BH^2 = 50^2 - 20^2
BH^2 = 2500 - 400
BH^2 = 2100
Чтобы найти длину отрезка BH, нужно извлечь квадратный корень из обеих сторон:
BH = √2100
Сокращая корень, получим:
BH = 10√21
Итак, длина отрезка BH равна 10√21.