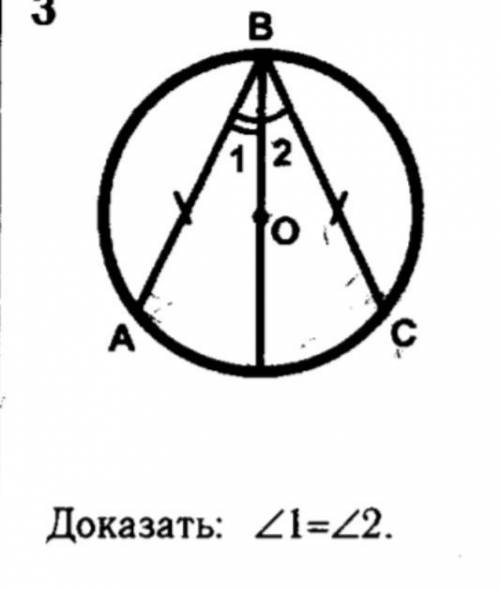
Дано : AB=CB Док-ть: угол 1=углу 2

Давайте решим эту задачу вместе. У нас дано, что отрезок AB равен отрезку CB.

Чтобы доказать, что угол 1 равен углу 2, мы можем использовать свойство треугольника, что сумма углов треугольника равна 180 градусов.

У нас есть треугольник ABC. Угол 1 и угол 2 - это два угла этого треугольника. Давайте предположим, что угол 1 и угол 2 не равны. Пусть угол 1 больше угла 2, то есть угол 1 > угла 2.

Теперь, рассмотрим треугольник CBA. Угол 1 является наибольшим углом в этом треугольнике (поскольку мы предположили, что угол 1 > угла 2). Что это означает?

Это означает, что сумма двух других углов треугольника CBA (угол 2 и угол BAC) должна быть меньше 180 градусов (поскольку угол 1 уже занимает большую часть 180 градусов). Но угол 2 и угол BAC должны вместе занимать 180 градусов, поэтому у нас возникает противоречие!

Таким образом, наше предположение было неверным. Угол 1 не может быть больше угла 2. Остается только один вариант - угол 1 и угол 2 должны быть равными.

Таким образом, мы доказали, что если AB равно CB, то угол 1 равен углу 2.