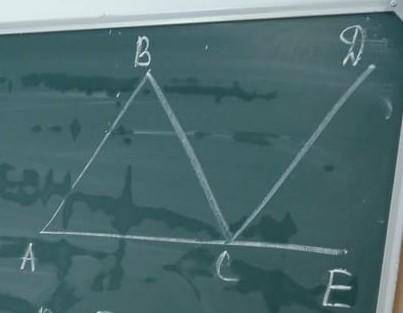
Дано: AB=BC, угол А 30°, угол DCE=1/5<BCE
докажите: AB || CD​

. .......................

Для доказательства, что AB || CD, мы можем использовать свойства параллельных линий и свойства углов.

Из условия задачи нам дано, что AB = BC и угол А равен 30°. Давайте рассмотрим треугольник ABC.

Обратим внимание на угол B. Так как треугольник ABC - равнобедренный, то угол B находится напротив равных сторон AB и BC. Следовательно, угол B также равен 30°.

Теперь обратим внимание на треугольник DCE, в котором у нас задан угол DCE, равный 1/5 угла BCE.

Для доказательства того, что AB || CD, мы должны найти соответствующие углы. Соответствующие углы - это углы, которые находятся на параллельных линиях и находятся в одной и той же позиции по отношению к пересекающейся прямой.

Обозначим угол BCE как угол X. Так как угол B равен 30°, то угол X равен 30°.

Также, у нас задан угол DCE = 1/5 угла BCE. Значит, угол DCE = 1/5 * 30° = 6°.

Теперь давайте рассмотрим треугольник CDE. У нас есть три угла: CDE, DCE и угол X (угол BCE).

Сумма углов в треугольнике равна 180°. Значит:
CDE + DCE + X = 180°
Следовательно:
CDE + 6° + 30° = 180°
CDE + 36° = 180°
CDE = 180° - 36°
CDE = 144°

Теперь давайте рассмотрим треугольник CDE и треугольник ABC. У нас есть два угла, которые соответствуют друг другу: угол CDE и угол B.

Это означает, что треугольники CDE и ABC подобны (по правилу соответствующих углов).

По свойствам соответствующих углов параллельных линий, у нас имеется следующее соотношение между сторонами этих треугольников:

CE/AB = DE/BC

Мы знаем, что AB = BC, следовательно, это соотношение перепишется как:

CE/AB = DE/AB

Заметим, что если мы удвоим DE (при этом CE останется прежней), то получится параллельная линия CD.

То есть, можно записать следующее:

2(DE/AB) = CD/AB

2(DE/AB) = 2(DE/AB) (тождество)

CD/AB = 2(DE/AB)

Зная, что DE/AB = CE/AB, мы можем записать следующее:

CD/AB = 2(CE/AB)

В результате, мы получили, что CD/AB = 2(CE/AB).

Это означает, что CD = 2CE. А так как мы знаем, что угол CDE равен 144°, то у нас есть два равных угла при вершинах C и E.

Таким образом, получаем, что треугольники EDC и BAC подобны (по правилу двух сторон и угла между ними).

Из подобия треугольников следует, что такие параллельные линии как AB || CD.

QED (что и требовалось доказать).