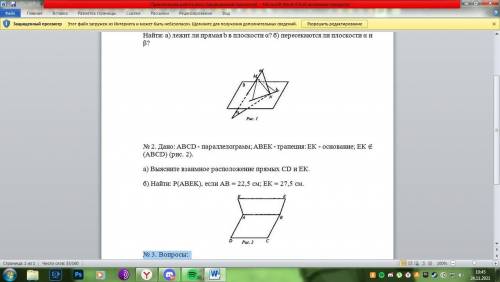
Дано: а и b - скрещивающиеся прямые; γ - плоскость, а ∉ γ, b ∈ γ. Точка M ∈ а, точка N ∈ b. Через а и N проведена плоскость α. Через b и М проведена плоскость β (рис. 1). Найти: а) лежит ли прямая b в плоскости α? б) пересекаются ли плоскости α и β?
Дано: ABCD - параллелограмм; АВЕК - трапеция: ЕК - основание; ЕК ∉ (ABCD) (рис. 2).
а) Выясните взаимное расположение прямых CD и ЕК.
б) Найти: Р(ABEK), если АВ = 22,5 см; ЕК = 27,5 см.
№ 3. Вопросы:
а) Какие две прямые в пространстве называются параллельными?
б) Сформулируйте признак параллельности прямой и плоскости.
в) Какие возможны случаи взаимного расположения прямой и плоскости?
г) Дан куб ABCDA1В1C1D1. Запишите четыре пары параллельных прямых.
д) Верно ли утверждение: если одна из двух параллельных прямых параллельна плоскости, то вторая прямая не пересекает эту плоскость.

юлка10    2   25.11.2021 08:03    16