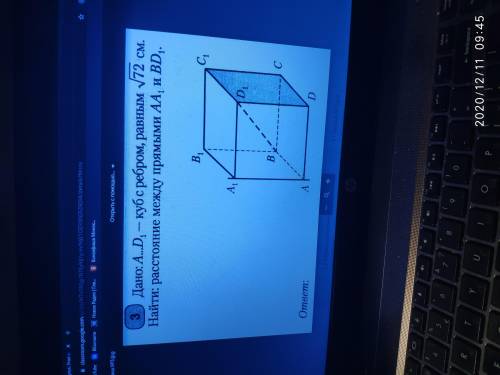
Дано:A...D1 -куб с ребром,равным√72см.Найти: расстояние между прямыми AA1 и BD1.

Для начала, давайте рассмотрим куб A...D1, чтобы понять, какие прямые нам нужно рассмотреть.

На рисунке мы видим, что куб A...D1 состоит из восьми вершин: A, B, C, D, A1, B1, C1 и D1. Задачей является нахождение расстояния между прямыми AA1 и BD1.

Для начала рассмотрим точки A, A1, B и D1. Мы знаем, что сторона куба равна √72 см. Чтобы найти координаты точек, используем равенство:

√72 = √(36 * 2) = √36 * √2 = 6√2.

Теперь у нас есть координаты точек A (0, 0, 0), A1 (0, 0, 6√2), B (6√2, 0, 0) и D1 (0, 6√2, 0).

Чтобы найти расстояние между прямыми AA1 и BD1, мы можем использовать формулу расстояния между двумя параллельными прямыми:

d = |(x2 - x1) * a + (y2 - y1) * b + (z2 - z1) * c| / √(a^2 + b^2 + c^2),

где (x1, y1, z1) и (x2, y2, z2) - координаты точек на прямых, a, b, c - коэффициенты.

Для начала найдем коэффициенты a, b и c для прямой AA1. Мы можем использовать координаты точек A (0, 0, 0) и A1 (0, 0, 6√2).

a = 0 - 0 = 0,
b = 0 - 0 = 0,
c = 6√2 - 0 = 6√2.

Теперь у нас есть коэффициенты a = 0, b = 0 и c = 6√2 для прямой AA1.

Теперь найдем коэффициенты a, b и c для прямой BD1. Мы можем использовать координаты точек B (6√2, 0, 0) и D1 (0, 6√2, 0).

a = 0 - 6√2 = -6√2,
b = 6√2 - 0 = 6√2,
c = 0 - 0 = 0.

Теперь у нас есть коэффициенты a = -6√2, b = 6√2 и c = 0 для прямой BD1.

Подставим коэффициенты в формулу расстояния между прямыми:

d = |(0 - 0) * 0 + (0 - 0) * 6√2 + (6√2 - 0) * 0| / √((-6√2)^2 + (6√2)^2 + 0^2)
= |0 + 0 + 0| / √(72 + 72 + 0)
= 0 / √(144)
= 0.

Таким образом, расстояние между прямыми AA1 и BD1 равно 0. Обе прямые являются параллельными и не пересекаются.