1. Математика
  2. Дано: |а|=4; |b|=1; угол между

Дано: |а|=4; |b|=1; угол между векторами а и b равен 60°. найдите cos a, a-угол между векторами а - b и b. нужно. заранее

Dhshssh Dhshssh    2   06.06.2019 13:00    311

Ответы
Fania2009 Fania2009  01.10.2020 20:36

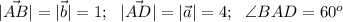
Дано:  |\vec {AB}| = |\vec b| = 1;~~|\vec {AD}| = |\vec a| = 4;~~\angle BAD=60^o

Найти : cos α - ?

По правилу параллелограмма разностью векторов является диагональ параллелограмма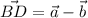  \vec {BD} = \vec a - \vec b

ΔABD : теорема косинусов

|\vec a - \vec b|^2=|\vec a|^2 + |\vec b|^2 - 2\cdot |\vec a|\cdot |\vec b|\cdot \cos60^o=\\ \\ ~~~~~~=4^2+1^2-2\cdot 4\cdot 1\cdot \dfrac12=13\\ \\|\vec a - \vec b|=\sqrt {13}

ΔABD : теорема косинусов

|\vec a|^2 = |\vec a-\vec b|^2 + |\vec b|^2 -2\cdot |\vec a-\vec b|\cdot |\vec b|\cos \angle ABD\\ \\ \\ \cos \angle ABD=\dfrac{|\vec a|^2 - |\vec a-\vec b|^2 - |\vec b|^2}{2\cdot |\vec a-\vec b|\cdot |\vec b|}=\\ \\ \\~~~~~~~~~~~~~~~=\dfrac{4^2-\sqrt{13}^2-1^2}{2\cdot\sqrt{13}\cdot 1}=\dfrac 1{\sqrt{13}}

∠KBD  и  ∠ABD  - смежные  ⇒  ∠KBD = 180°-∠ABD

\cos \angle KBD = \cos (180^o-\angle ABD)=-\cos \angle ABD=-\dfrac 1{\sqrt{13}}\\ \\ \\ \boxed{\boldsymbol{ \cos \alpha =-\dfrac 1{\sqrt {13}}}}


Дано: |а|=4; |b|=1; угол между векторами а и b равен 60°. найдите cos a, a-угол между векторами а -
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Yuliya12222222222 Yuliya12222222222  09.08.2019 02:00
Девочка прочитала в 3 раза меньше страниц чем ей осталось прочитать всего в книге 176 страниц сколько страниц ей осталось прочитать можно поподробнее объяснить...
лиса266 лиса266  09.08.2019 02:00
Объясни смысл пословицы: кто слишком долго думает о том, чтобы делать добро, тому нет времени быть добрым...
Negogda Negogda  09.08.2019 02:00
Стоимость товара в первый раз снизилась a%,а во второй-на b%от новой цены.в каких случаях в результате стоимость товара составила 60% исходной цены?...
narigeevag71mariy narigeevag71mariy  09.08.2019 02:00
1.какой знак препинания предшествует элементу .- точка и тире , запятая ; точка с запятой : двоеточие косая черта 2. найдите ошибку в библиографическом описании байгереев,м....
Snomeli Snomeli  09.08.2019 02:00
9+x=6 нойдите х после девять плюс (+)...
Big1fbfb Big1fbfb  09.08.2019 02:00
Две колхозницы шли в город и встретили на дороге пять колхозниц сколько всего колхозниц шли в город...
с1413а с1413а  09.08.2019 02:00
Решите уравнение ((171-9х): 15+174): 45=4...
Moew Moew  09.08.2019 02:00
Твір есе на тему політика це мистецтво можливого...
cneze cneze  09.08.2019 02:00
Масса 3 арбузов составляет 19 целых 23\24 кг.масса 1 и 2 - 13 целых 3/16кг,а 1 и 3 -12 целых 3/16 кг. найдите массу каждого арбуза....
tarlavinEgor tarlavinEgor  09.08.2019 02:00
:функция задана формулой y=x29y=x29. сравните с нулем значения этой функции при x=−7; 0; 2x=−7; 0; 2. выберите правильный ответ: 1) (−7)29 0; 029=0; 229 0(−7)29 0; 029=0;...

Популярные вопросы