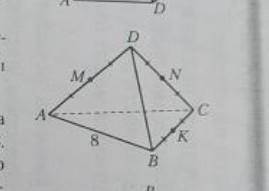
Дана треугольная пирамида DABC, все ребра которой равны 8. Точки M, N, K - середины ее ребер AD, DC, BC. Найдите периметр сечения тетраэдра между точками C и

Для решения этой задачи, нам необходимо найти периметр сечения тетраэдра между точками C и K.

Перейдем к решению:

1. Найдем длину отрезка CM. Точка M - середина ребра AD, поэтому отрезок CM является медианой треугольника ADC. В треугольнике ADC медиана делит сторону на две равные части, а значит отрезок CM будет равен половине стороны AD.
Длина отрезка AD равна 8, поэтому длина отрезка CM будет равна 8/2 = 4.

2. Аналогично, найдем длину отрезка CK. Точка K - середина ребра BC, поэтому отрезок CK является медианой треугольника ABC. В треугольнике ABC медиана делит сторону на две равные части, а значит отрезок CK будет равен половине стороны AB.
Длина отрезка AB равна 8, поэтому длина отрезка CK будет равна 8/2 = 4.

3. Теперь найдем длину отрезка MN. Отрезок MN является медианой треугольника CDB. В треугольнике CDB медиана делит сторону на две равные части, а значит отрезок MN будет равен половине стороны CD.
Длина отрезка CD равна 8, поэтому длина отрезка MN будет равна 8/2 = 4.

4. Так как сечение проходит через точки C и K, нам необходимо найти периметр треугольника CKM. Для этого сложим длины сторон CK, KM и MC.
CK = 4 (мы уже вычислили это ранее)
KM = MK (по свойству симметрии относительно точки N)
= MN (по свойству симметрии относительно точки M)
= 4 (мы уже вычислили это ранее)
MC = CM (по свойству симметрии относительно точки K)
= 4 (мы уже вычислили это ранее)

Теперь сложим стороны треугольника CKM для получения периметра:
Периметр CKM = CK + KM + MC = 4 + 4 + 4 = 12.

Таким образом, периметр сечения тетраэдра между точками C и K равен 12.